程序分析技术

基本概念¶

分析（analysis）与验证（verification）¶

在 Paper 中常有两个概念：分析和验证，验证常以形式化验证（formal verification）的形式出现。

首先，此处的讨论分析和验证应用的对象都为程序（program）。

抽象的说，formal verification 是把程序转化到某个数学域上，同时把我们需要满足的某个需求或者特性（property）转换到同一个数学域上，最后验证一下二者是否匹配。

program analysis 也能以这种方式定义，因为在具体应用的时候，总能找到对应的数学域，比如控制流或者数据流，也总能根据我们要分析的问题来抽象出 property，比如数据流需要满足某种传播条件。

所以可以认为分析与验证是同一个东西。

Reference: https://www.zhihu.com/question/438252679

当从具象化的层面理解，程序分析通常是对目标程序的控制流图（CFG）进行分析，而验证更多的是判断代码的行为 (behaviour) 与设计指标 (specification) 是否匹配。

静态分析

TODO sound 等等

编译器、AST、IR¶

编译器¶

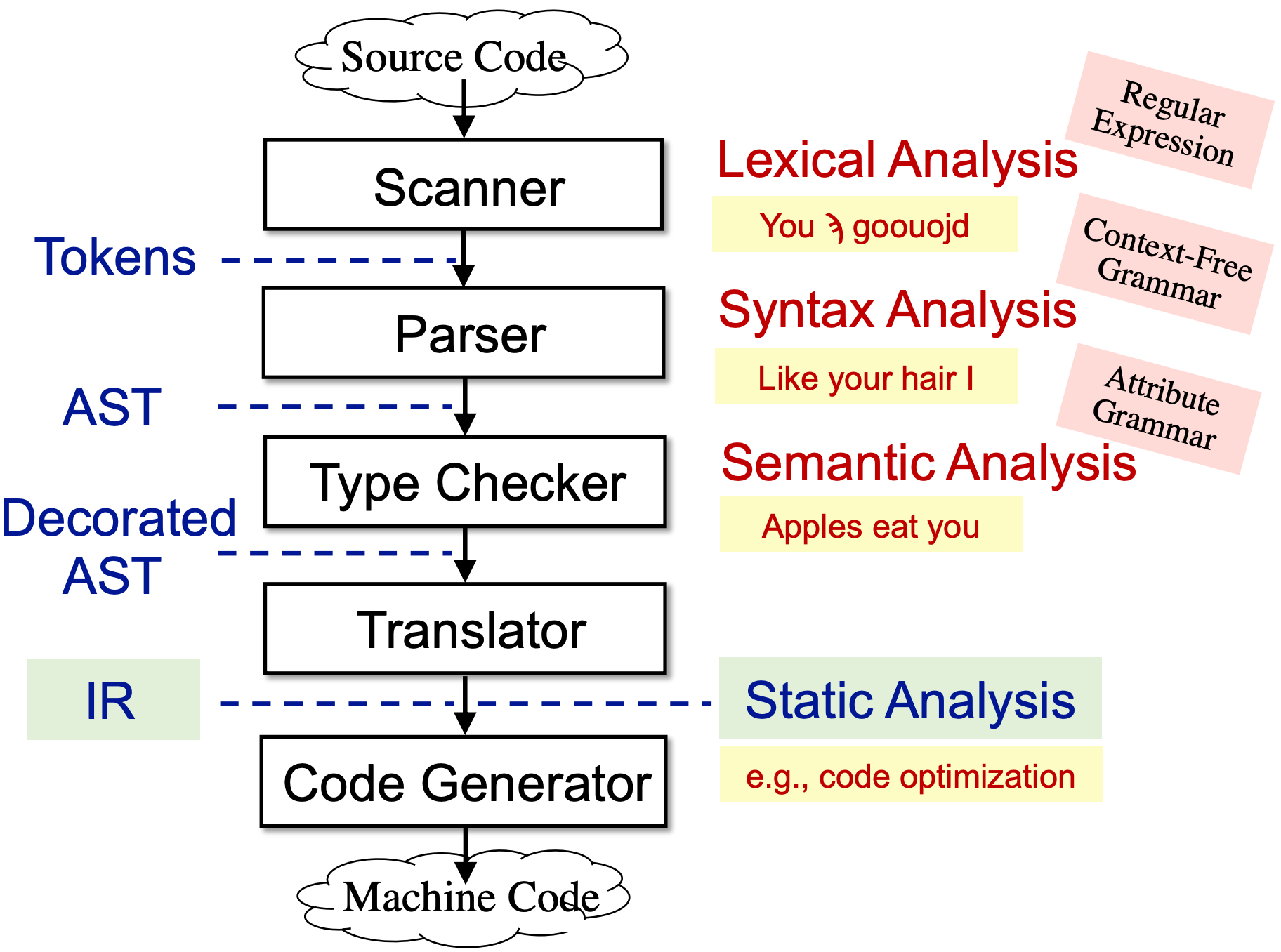
从编译器讲起，编译器分为前端和后端，前端负责将源码编译为中间表示，后端负责将中间表示编译为机器代码（01 二进制），具体流程如下：

Scanner，词法分析器，接受源码输出字符流。
Parser，语法分析器，接受字符流，输出 AST
Type Checker：语义分析器，进行类型检查等工作，输出也是 AST
Translator：编译器中端将 AST 翻译为多种中间表示（IR），常用的如三地址码。静态分析通常基于 IR 进行！
Code Generator：编译器后端将 IR 翻译为机器代码

Compilers-and-Static-Analyzers

AST¶

抽象语法树（AST）是源代码的抽象语法结构的树状表示，树上的每个节点都表示源代码中的一种结构，之所以说是抽象的，是因为抽象语法树并不会表示出真实语法出现的每一个细节。

在具体实现的过程中，抽象语法树，其实就是用树状结构表示语法结构，也没有说必须是什么形式，只要能忠实地反映出源码的格式即可。

Java Parser 提供了 Yaml、XML 和 Graphiz dot 等格式描述 AST，也有其他工具支持输出 Json 格式的 AST，例如 Coverity。

在一般文献中，都是画一个树状结构出来：

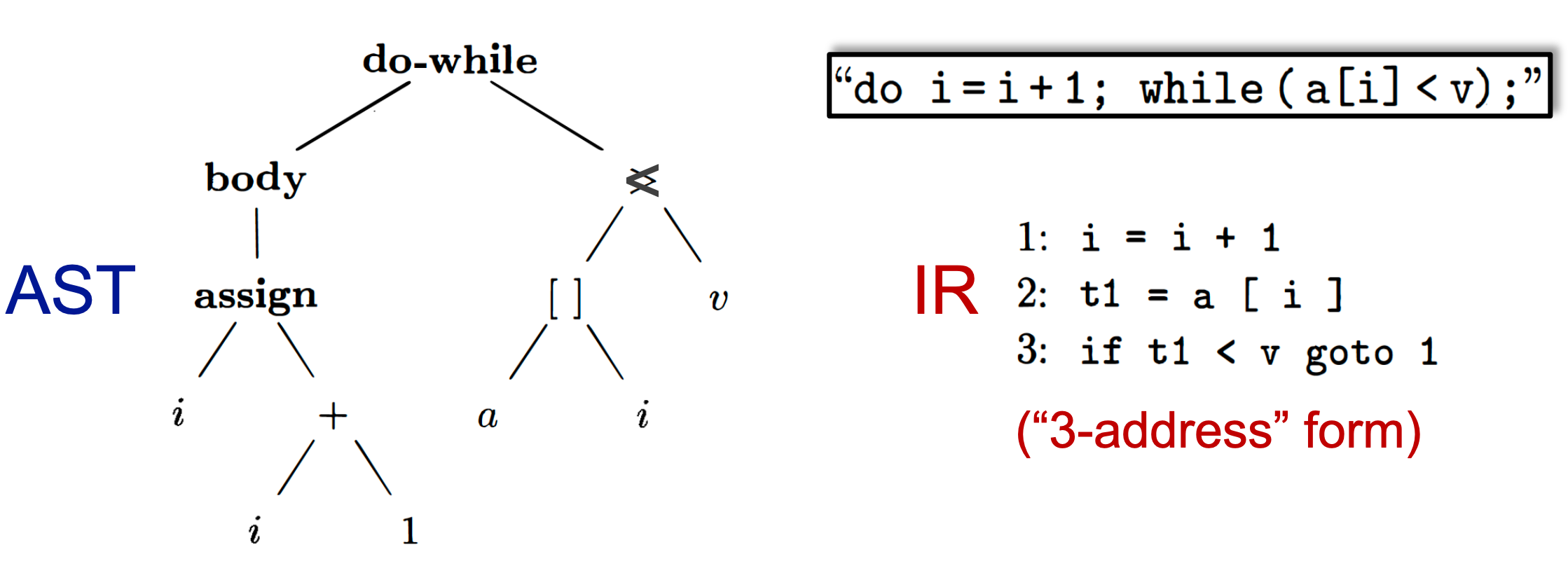
AST-IR

相比于 IR，AST 更 high-level，更接近程序结构，更依赖于源程序信息。

IR¶

通常静态分析基于中间表示（IR）进行，IR 有很多的形式，例如三地址码（3AC）、静态单赋值形式（SSA），其中三地址码是最常用的形式，例如目前最流行的 Java 静态分析框架 Soot ，其 IR 是 Jimple：typed 3-address code。

IR 与 AST 的区别：

IR 是 AST 进一步的抽象，更接近机器语言，可以认为和语言无关，是连接前后端的一种中间表示，因此当编程语言升级时（Java7 - Java8 新增 lambda 表达式、函数引用等特性），对应的 AST 必定新增节点，而 IR 则基本稳定不会发生变化。
AST 为了体现源码的程序结构，往往比较复杂，而三地址经过处理，一般比较紧凑，简单。例如 for、while、do while 等循环方式在 AST 层面完全不同，但在 IR 层面是相同的，即 IR 往往体现了控制流（control flow）信息，而 AST 不会。
IR 与语言无关，在部分静态代码分析工具实现时，会对不同语言的 IR 实现同一个分析引擎，只是通过开发不同语言的规则，实现对不同语言的能力的覆盖，而 AST 是无法做到这一点的。

需要知道 IR 在静态分析中是极其重要的，而三地址码更是被认为是静态分析的基础之一。

IR 的生成、选择及应用方式¶

静态程序分析有基于源码的程序分析和基于二进制的程序分析。相应的生成中间表示的方法不同：

基于源码的程序分析，主要应用到了编译原理相关的技术，是正向的 IR 的生成。
基于二进制的程序分析，主要需要对二进制程序进行反汇编，是逆向的 IR 生成。

静态代码分析工具的检查方法主要有面向程序结构的检查和基于数据流的检查。相应的选择的 IR 类型也不同：

面向程序结构的检查，一定是基于 AST 进行的检查，有时候需要结合 Token 和符号表一起检查；
基于数据流的检查，一般都是在三地址码（或 SSA）形式的中间表示上面分析，也可以在 AST 上面进行分析。

学术界通常选择三地址码作为 IR，而工业界如 coverity 和 fortify 这样的头部静态程序分析工具，都是在 AST 上面执行的数据流分析

事实上，静态分析工具在执行分析时，不会直接在 IR 上进行分析，而是在中间表示上进行各种抽象，从而简化我们的分析：

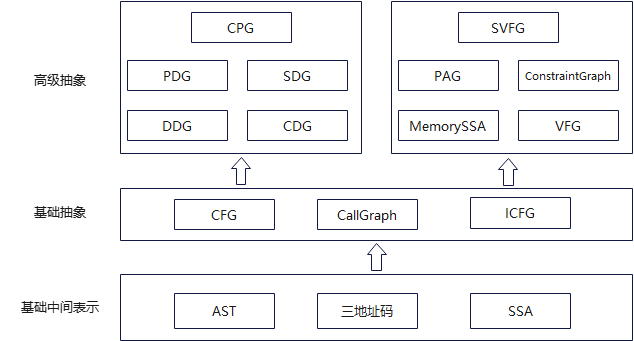
static_abs

最底层是输入的中间表示，通常如果有需要，可以进行序列化处理，然后直接读入，例如 clang 可以 dump AST，llvm 的 bc 文件就是一种 SSA 形式的中间表示；
中间的一层是在中间表示上生成的数据表示，一般基于中间表示执行数据流分析时，都需要生成这部分结构；
最上面的一层，是当前比较典型的两种比较高级的抽象形式。对 CPG 相关的概念，最初是在 joern 工具中引入的，综合了各种代码表示，并放到图数据库中，对 SVFG 相关概念，在 SVF 中引入的，并且，基于该框架，实现了一种基于 SVFG 的 MemoryLeak 的检查工具。

控制流图（CFG）与基础块（BB）¶

在很多静态分析工具的开发实践中，将 BB、CFG 的构造，和 IR（3AC、SSA）的生成，放在相同阶段，因此也可以将 CFG 也理解为一种中间表示，当然也有资料将 CFG 不当做 IR。

CFG 是静态分析的基本结构，其节点可以是单独的语句，也可以（通常）是一个基本块（BB），是一个有向图。

语句通常是三地址码（a = b + c），但在以太坊的静态分析软件 Oyente 中，基本块中的语句是由二进制代码反汇编得到的汇编语句（例如 PUSH 0X01、JUMP）

BB 是满足下列关系的语句的最大序列集合：

只可以从 BB 中的第一条指令进入
只可以从 BB 中的最后一条指令退出
BB 中的语句必须按照顺序依次执行

CFG 可以用一个三元式描述：G=(N, E, n0)

其中：

N：表示所有基本块节点的集合；
E：表示所有边的集合；
n0：表示首节点。

CFG 具有如下的两条性质：

CFG 必然有唯一的一个入口点；
首节点必然支配 CFG 中其他的所有节点（即从首节点到 CFG 上其他任何一个节点都有一条路可以连通）。

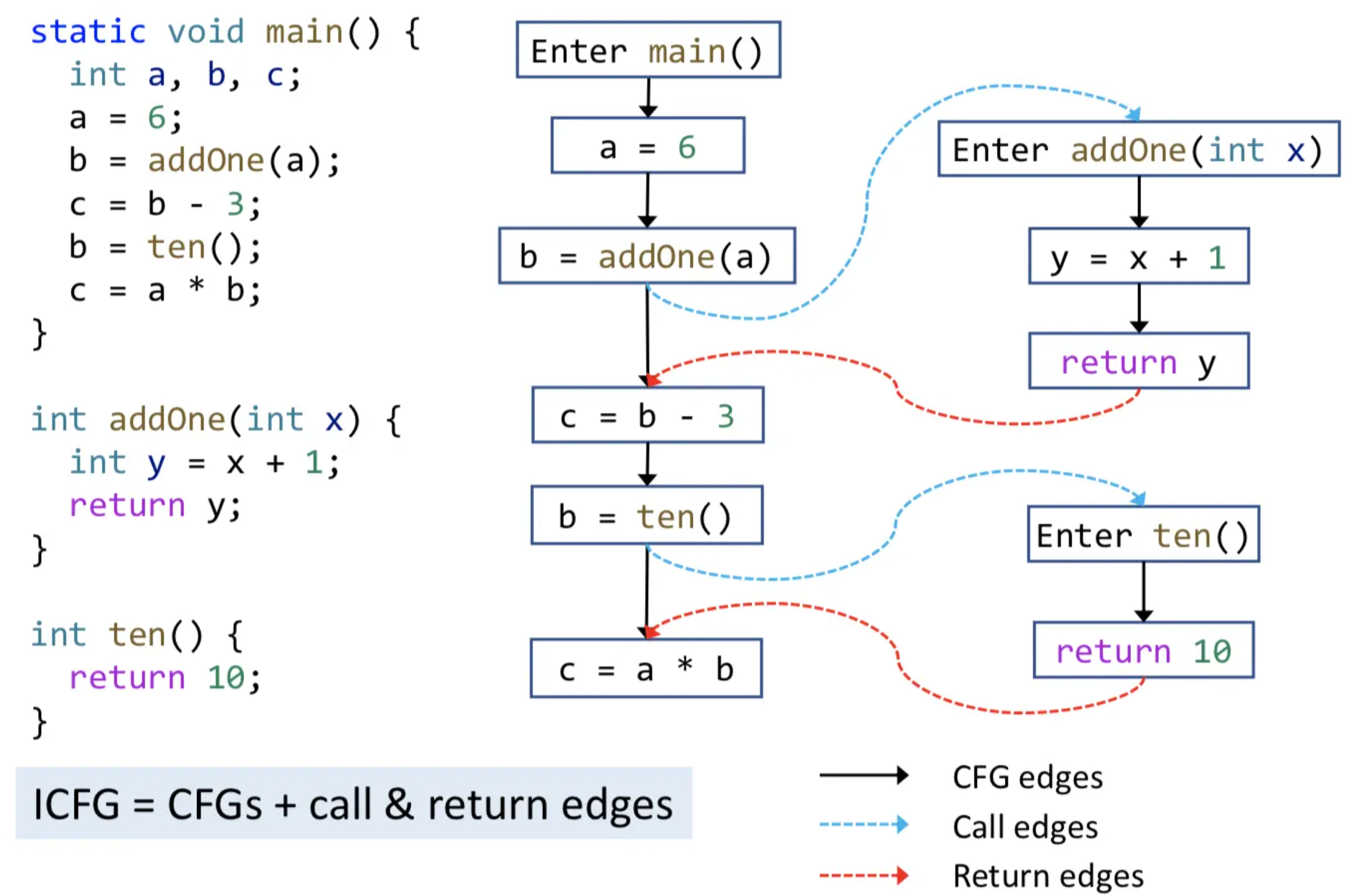
注意到 CFG 只能用于分析单个函数内的控制流转换，涉及到跨越函数边界的控制流则无法分析，因此引入 CG 和 ICFG。

调用图（CG）与过程间控制流图（ICFG）¶

CG：本质是调用边的集合，从调用点（call-sites）到目标函数（target methods / callees）的边。

CG_example

ICFG = CFG + (Call edges + Return edges)

Call edges：连接调用点和目标函数入口
Return edges：从 return 语句连到 Return site（Call site 后面一条语句）

ICFG_example

约束求解¶

约束求解问题，可以形式化表示为一个三元组的形式 $P=<V, D, C>$，其中的三个部分，含义分别为：

$V$：变量的集合，表示为 ${v_1, v_2, ..., v_n}$ ；
$D$：变量的值域的集合，即每个变量的取值范围，即变量 $v_i$ 需要在其值域 $d_i$ 内取值；
$C$：约束条件的集合，每个约束条件包含中一个或者多个变量，若 $c_i $ 中包含 $k$ 个变量，则称该约束是这 $k$ 个变量集合上的 $k$ 元约束。

约束求解就是基于这一系列的约束问题，求出来一个解，这个解对所有的约束都满足，并且在自己的值域范围内，如果有这样的一个解，就说这个约束问题是可满足的，否则，就说这个约束问题是不可满足的。

当前，主流的约束求解器主要有两种理论模型：SAT 求解器和 SMT 求解器。

SAT：布尔可满足性问题¶

SAT（Satisfiability, SAT）是 NP 问题，其定义如下：

sat

对于给定 CNF 表达式 $Φ$，求解合适的 $x_i$ 的值，使得 $Φ$ 为 $true$。可以看到，想要让 $Φ$ 为 $true$，必须每个 $C_i$ 都为 $true$，即每个 $C_i$ 中必须有一个 $x_i$ 为 $true$。

SAT 问题，求解的变量的类型，只能是布尔类型，可以解决的问题为命题逻辑公式问题。

SMT：可满足性模块理论¶

因为 SAT 求解器只能解决 命题逻辑公式 问题，而当前有很多实际应用的问题，并不能直接转换为 SAT 问题来进行求解，于是后来提出了 SMT（Satisfiability modulo theoris）理论。

SMT 求解器的求解范围从命题逻辑公式扩展为可以解决 一阶逻辑 所表达的公式。SMT 包含很多的求解方法，通过组合这些方法，可以解决很多问题。

我理解 SAT 的表达式 $Φ$ 中只有逻辑符号，而 SMT 的表达式中可以出现其他符号，如函数、常量等。

当前，已经有大量的 SMT 求解器（当然一般都同时支持 SAT 求解），例如微软研究院研发的 Z3 求解器、麻省理工学院研发的 STP 求解器等，并且 SMT 包含很多理论，例如 Z3 求解器就支持空理论、线性计算、非线性计算、位向量、数组等理论。

Z3 求解器¶

Z3 求解器是微软研究院开发并开源的一款 SMT 求解器，Z3 求解器可应用于约束求解，作为其他应用的底层工具，在定理证明、程序验证的项目中被大量使用，例如 SAGE、LLVM、KLEE 等。

Z3 致力于解决程序验证和软件分析中的求解问题，而且性能优越，提供的 API 非常简洁，且支持多种语言（C/C++, .NET, OCaml, Python, Java, Haskell）是很多静态代码分析工具的首选。

SAT Bool 表达式计算

from z3 import *
a, b, c = Bools('a b c')
s = Solver()
s.add(And(And(Or(a, Not(b)), Or(b, c)), Or(c, Not(a))))
print(s.check())
print(s.model())

a，b 和 c 分别都是 bool 表达式，在此进行的运算为 $φ=(α∨¬β)∧(β∨γ)∧(γ∨¬α)$ 取值为 $true$ 时的各变量取值，此处为 SAT 问题求解，其运算如下：

sat
[a = False, b = False, c = True]

SMT 一阶逻辑运算

基于 Z3 可以进行大量的数值运算、数值比较、数值表达式操作等，支持整型、浮点型等各种操作，支持各种算术运算，支持算术运算、不等式比较构成的 bool 表达式的各种组合操作，最后求解出具体的数值。

算数运算例子：

from z3 import *
x, y, z = Ints('x y z')
s = Solver()
s.add(x + y > 4)
s.add(z == x + 3)
s.add(x * x + y * y < 30)
s.add(z < 9)
print(s.check())
print(s.model())

如上，是关于 x，y，z 三个 int 类型的数字的一系列不等式的约束求解（含义非常简单，不再介绍），最后运算的结果如下：

sat
[z = 3, y = 5, x = 0]

此外，Z3 还能用于表达式简化、位运算、数组操作等

约束求解的应用¶

例如在符号执行中，使用约束求解器（e.g. Z3）对当前路径约束求解，得到 测试输入；如果程序输入这些实际值，就会在同样路径结束。

在 Oyente 中，首先对合约构建 CFG，随后对合约进行符号执行，符号执行从 CFG 的 entry node 开始，并使用 Z3 作为符号执行的约束求解器，每当遇到条件跳转时，计算路径约束是否有解，以此判断该路径是否可行。

Reference:

什么是 SMT (satisfiability modulo theories)？

约束求解

形式化验证¶

形式化常用于硬件、系统内核等较为稳定的场合，而一般软件开发迭代太快，因此形式化验证就不太适用，因为成本过高，且一般的软件分析方式如模糊测试、符号执行已经足够使用。

而在区块链 DAPP 上，由于代码一经上链无法修改，因此有必要使用形式化验证来严格保证代码的安全性。

那么什么是形式化验证？

根据我的理解，提供代码和规约（specification），此处规约是可选的，形式化验证工具会将其转换为数学公式（也可能先将代码和规范转换为对象模型，再将对象模型转换为数学公式），交给定理证明器，定理证明器通过数学推理和证明，确定代码是否符合规约。

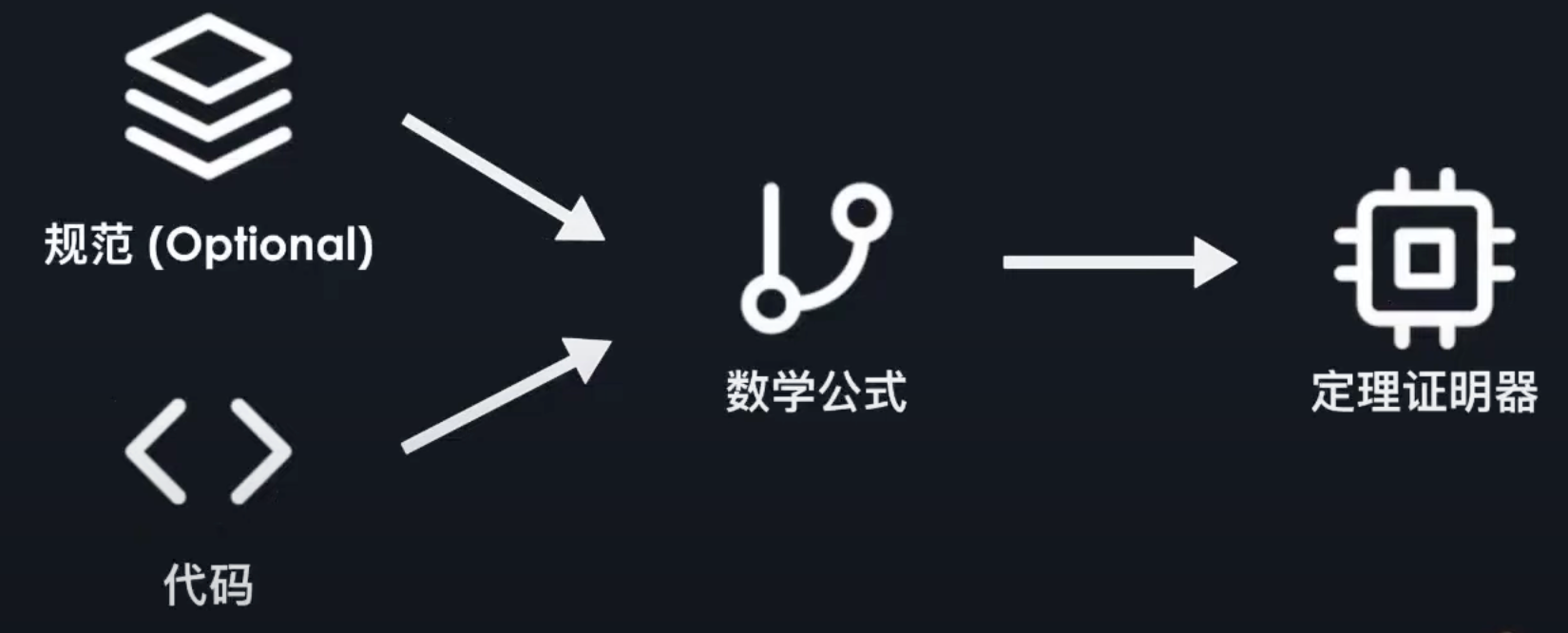
formal_verification

很多形式化验证的问题可以转化成公式满足性问题，也就是 SMT，因此可以通过 Z3 等求解器进行计算。例如 Hawblitzel 等人将源程序翻译到中间语言 Boogie，在 Boogie 上开展验证,并将生成的验证条件交给 Z3 自动证明。

对象模型

在形式化验证中，对象模型（Object Model）是指要进行验证的系统或软件的抽象模型。对象模型可以是任何形式的抽象表示，比如状态机、转换系统、时序逻辑电路等等，具体取决于要验证的系统的特性和需求。

在使用定理证明器进行形式化验证时，需要将对象模型表示为逻辑公式的形式，然后使用定理证明器来证明或反驳这些公式。

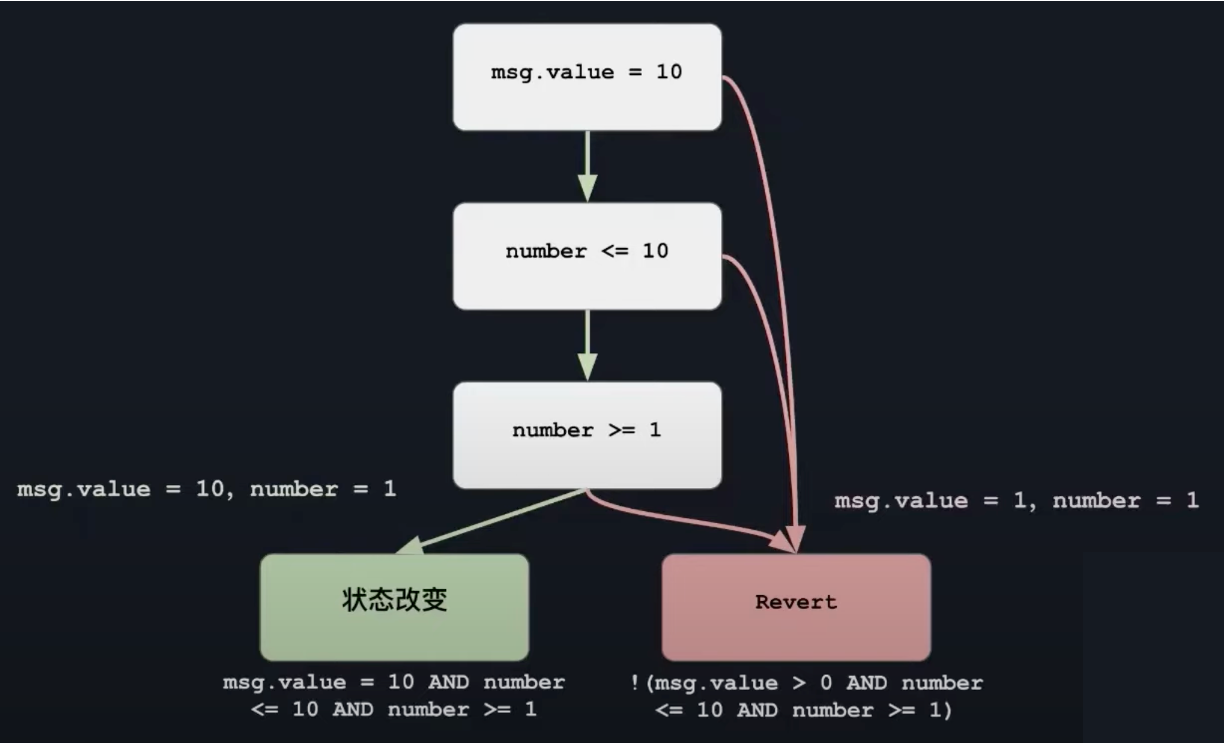
例子

function bet(uint256 number) public payable {
        require(msg.value = 10, "付款应该等于 10");
        require(number <= 10, "Number 应该小于等于 10");
        require(number >= 1, "Number 应该大于等于 10");
        totalBets += msg.value;
        bets[msg.sender] = number;
}

将上述代码转换为控制流图，当满足左下方公式时，状态将发生改变，当满足右下方公式时，将触发 Revert，图中也给出了具体的输入样例。

bet_cfg

于是，我们可以用公式表达整个程序，即将代码翻译为数学表达式：

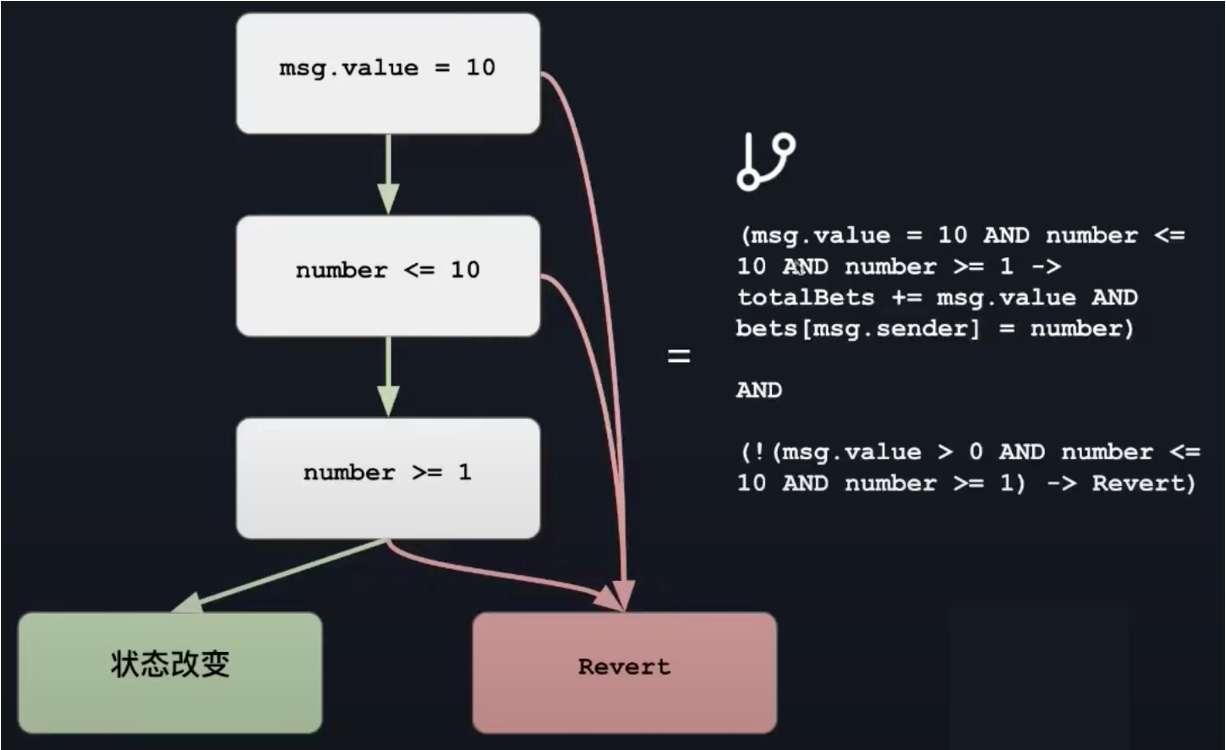
code_to_math

$AND$ 左侧的公式含义是，当满足 $msg.value = 10 \ AND \ number<= 10 \ AND \ number >=1$ 时，将导致程序状态的改变，也就是 $totalBets += msg.velu \ AND \ bets[msg.sender] = number$，$AND$ 右侧同理，满足条件时将触发 revert。

$AND$ 两侧的表达式不管 $msg.value$ 和 $number$ 的值是多少，始终是为 true，因此二者进行 $AND$ 后也始终为 true。

也就是说，在没有任何约束的情况下，形式化验证可以生成任意的数字（我理解就是生成测试样例， $msg.value$ 和 $number$ 可能是任意数字）

随后我们加入规范（specification），它描述了代码应该如何运行。

spec:
    bets[msg.sender] < 10

此时，将会形式化验证工具将判断输入的代码是否符合规范，也就是代码执行后，是否满足 $bets[msg.sender] < 10$，当然，此处是不满足的，因为当 $number=10, msg.value=10$ 时，代码执行后， $bets[msg.sender] = 10$。

那么具体是如何判断的呢？首先我们要将规范和之前代码转换成的数学公式联系起来：

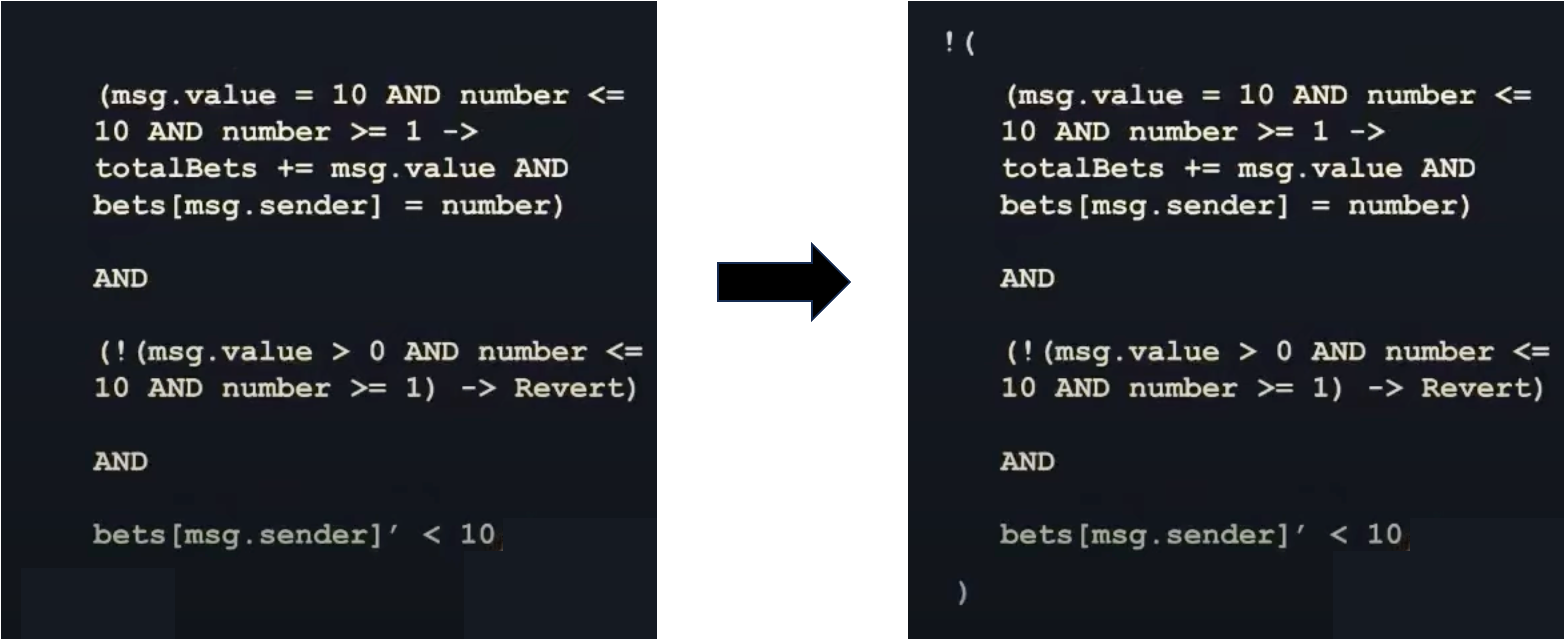
formal_verification_fou

首先看左侧，只是将规约与代码的公式表达简单的用 $AND$ 连接，此时如果用 SMT 求解器求解，是无法获取反例的（$number=10, msg.value=10$），因此我们往往会取反，此时当求解器的结果是 SAT 时，就表明找到了不符合规范的反例，若结果是 UNSAT，则说明代码符合规范。

这里我们找到了反例 $number=10, msg.value=10$ ，假设我们的规范是正确的，那么我们要修改代码：

// old
require(number <= 10, "Number 应该小于等于 10");
// new
require(number < 10, "Number 应该小于 10");

此时再次运行形式化验证器，SMT 求解器将返回 UNSAT，说明代码是符合规范的。

Reference

Solidity 形式化验证

形式化验证 | 青年学者计划

Boogie¶

https://www.microsoft.com/en-us/research/project/boogie-an-intermediate-verification-language/

Boogie is a modeling language, intended as a layer on which to build program verifiers for other languages.

Boogie is also the name of a tool. The tool accepts the Boogie language as input, optionally infers some invariants in the given Boogie program, and then generates verification conditions that are passed to an SMT solver. The default SMT solver is Z3.

Move Prover¶

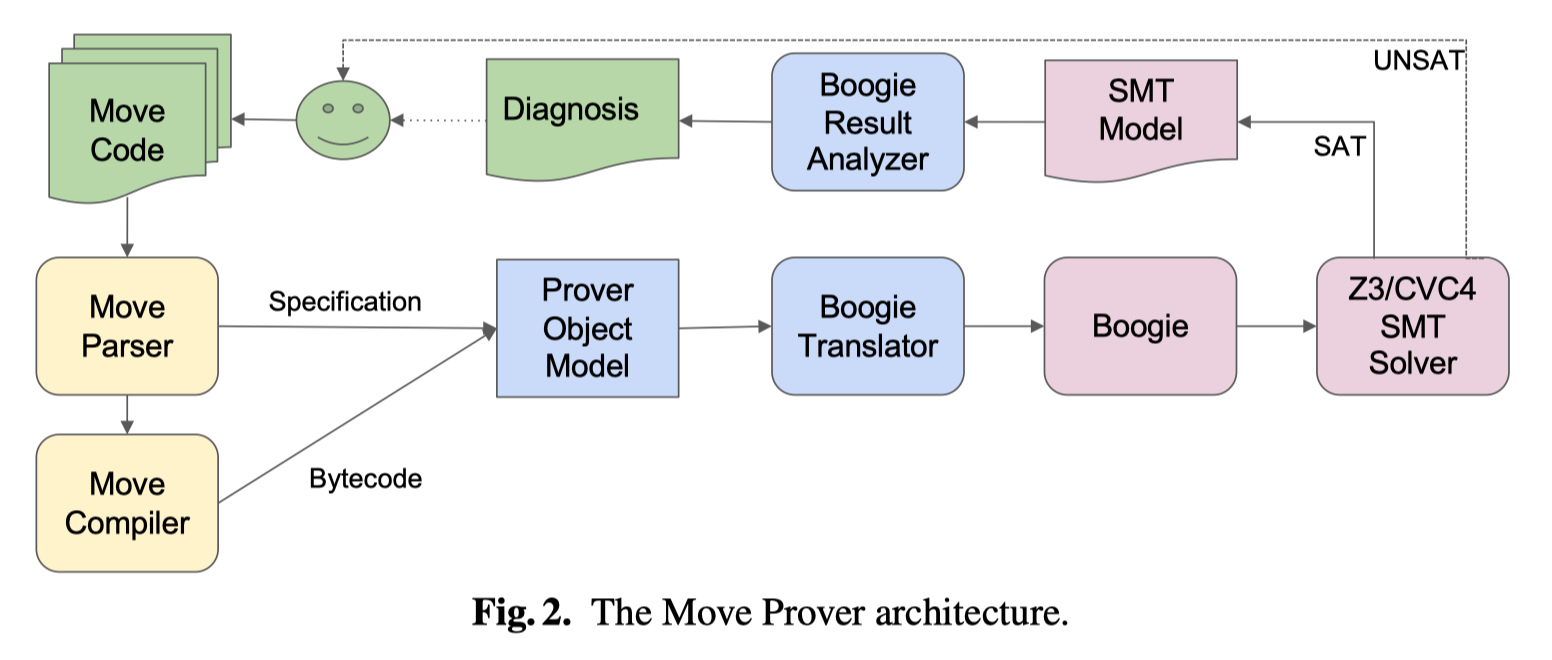
move_prover_architecture

上图是 Move Prover 的架构，输入：Move source code annotated with speciﬁcations

从输入的 Move 源代码的注释中提取规范
将 Move 源码翻译为字节码（bytecode）
从字节码中删除所有堆栈操作，并将其替换为对局部变量的操作，称修改后的字节码为：stackless bytecode
将 stackless bytecode 抽象为 prover object model
解析提取出来的规范，并将其加入到 prover object model 中
将最终确定的 prover object model 翻译为 Boogie intermediate veriﬁcation language (IVL)
Boogie 程序生成 SMT 公式，使用 SMT 求解器（如 Z3）进行检查，如果是 UNSAT，则规范成立，否则，报错。

为什么是 UNSAT 说明规范成立？

因为我们是寻找不满足规范的样例，因此如果 UNSAT，则说明找不到这样的样例，也就是不违反规范，此时说明程序没有问题。

如果结果为 SAT，则说明 Z3 找到了不满足规范的样例。

其他¶

反编译 VS 反汇编

反汇编：将可执行的文件中的二进制经过分析转变为汇编程序。
反编译：反编译：将可执行的程序经过分析转变为高级语言的源代码格式，一般完全的转换不太可能，编译器的优化等因素在里面。

过程内分析（Intraprocess analysis） VS 过程间分析（Interprocedural analysis）

过程内分析：仅在单个函数内分析，通过 CFG 即可进行，通常用于局部优化，例如寻找未使用的变量、常量折叠、死代码消除等。
过程间分析：在多个函数中进行分析，考虑程序的完整结构，可用于更广泛的优化，例如函数内联、指针分析、数据流分析等。

常用技术¶

数据流分析¶

参见 /corse/软件分析

CFG（control flow graphs）是静态分析的基本结构，其节点通常是基本块（basic block），基本块的首个指令是 leader 指令，最后一个指令是跳转指令（跳转的目的地是 leader 指令，此时也就是基本块）。

数据流分析就是分析数据在 CFG 中的流动，例如可以进行 Reaching Definitions Analysis 等分析。程序到达不定点时终止。

数据流分析是软件分析中静态分析中比较重要的一部分，结合符号执行、污点分析、fuzzing 技术可以发挥巨大的效用。

指针分析¶

这个在 /corse/软件分析的课程中也有提到，不过我还没学。

指针分析:https://zhuanlan.zhihu.com/p/79804033

20230714 update:

指针分析解答的是一个指针可能指向哪个对象的问题

别名分析：别名分析解答的是两个指针是否能指向同一个对象的问题，如果是就认为二者互为别名。

指针分析有两个指标即精度（precision)和速度（efficiency)，我们需要根据实际情况在这两者中进行取舍，有很多因素会影响这两个指标：

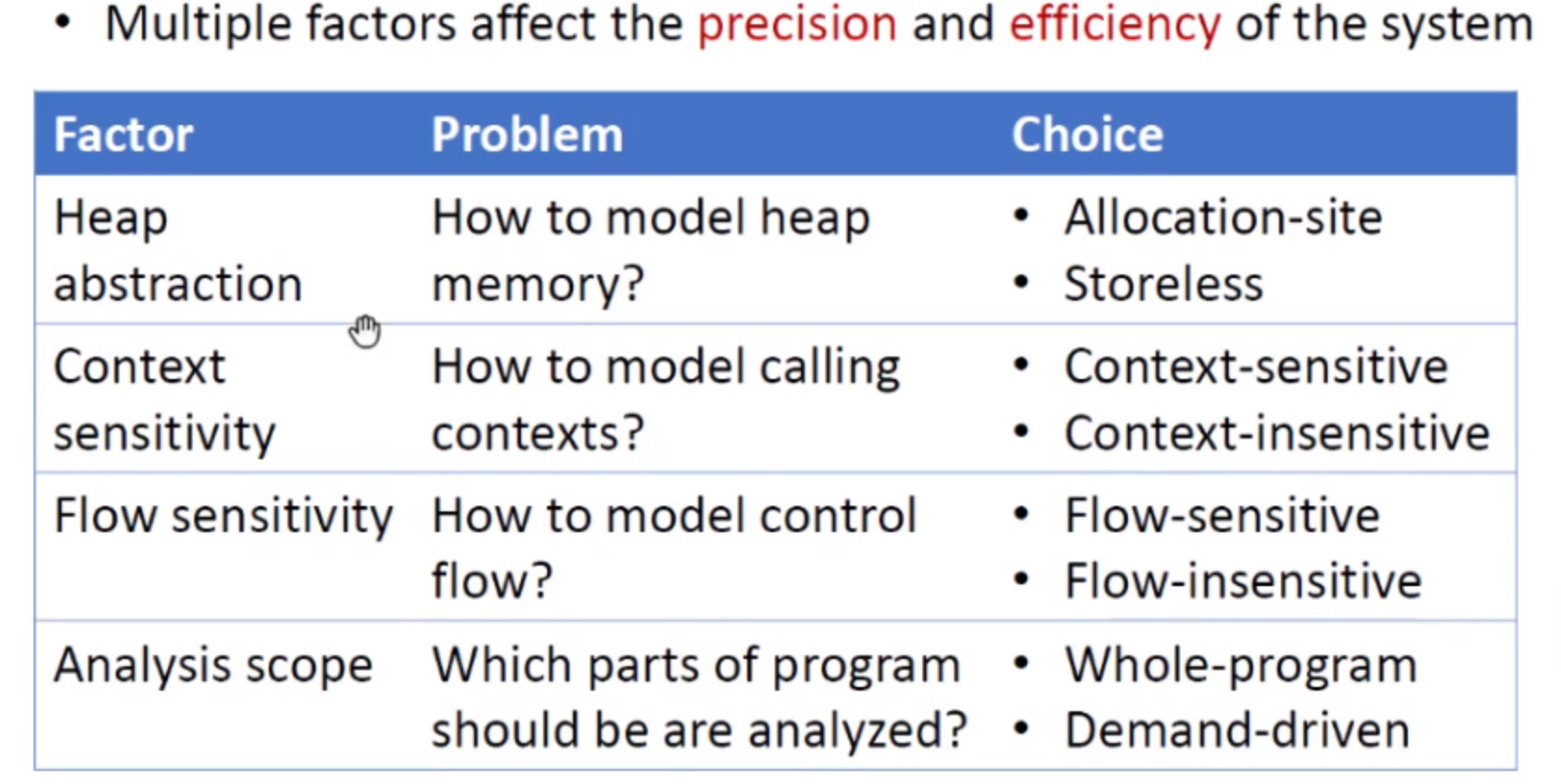
指针分析影响因素

更多：https://www.cnblogs.com/crossain/p/12767883.html

符号执行¶

诞生于 70 年代中期，其设计意图是用于测试软件是否会违反“给定特性”：

安全特性：例如缓冲区溢出、除零、空指针解引用等
功能特性

符号执行采用抽象的符号代替精确值（如数字 1）作为程序输入变量

符号执行维护 符号状态( symbolic state ) σ 和 符号路径约束( path constraint ) PC

σ 表示变量到 符号表达式 的映射，初始化为空映射。
PC 是符号表示的不含量词的一阶表达式，用来表示路径约束条件。初始化为 true。

1 int twice(int v) {
2    return 2 * v;
3 }
4
5 void testme(int x, int y) {
6     z = twice(y);
7     if (z == x) {
8         if (x > y + 10)
9             ERROR;
10    }
11 }
12
13 int main() {
14     x = sym_input();
15     y = sym_input();
16     testme(x, y);
17     return 0;
18 }

符号状态 σ

每当遇到赋值语句，就会向符号状态 σ 中添加一个映射。

以上述代码为例，当程序执行 line 14 和 line 15 时，符号执行采用抽象的符号代替精确值作为程序输入变量，也就是说，将程序输入变量 x，使用抽象的符号代替，如 x₀

在执行完 line 14 和 line 15 赋值后，符号状态 σ 中添加映射：σ = { x→x₀, y→y₀ }，此时 x₀和 y₀称为 不受约束的符号值。

当执行到 line 6 时，再次添加新的 kv 键值对，此时符号状态 σ 为：σ = { x→x₀, y→y₀, z→2y₀ }

符号路径约束 PC

每当条件语句 if (e) S1 else S2，PC 更新为 PC∧σ(e)，表示 then 分支；同时生成新的路径约束 PC'，并且初始化为 PC∧¬σ(e)，表示 else 分支。

以上述代码为例，当程序执行 line 7 时，建立了两个符号执行实例，路径约束 PC 分别为：2y₀ = x 和 2y₀ ≠ x

当执行到 line8 时，再次建立两个新的符号执行实例，路径约束 PC 分别为：(2y₀ = x)∧(x₀ > y₀ + 10) 和 (2y₀ = x)∧(x₀ ≤ y₀ + 10)

执行结束

符号执行遇到 exit 或者 error（比如程序崩溃或者违反断言），当前实例将会终止。

此时利用 约束求解器（e.g. 使用可满足性模理论，SMT）对当前路径约束求解，得到 测试输入；如果程序输入这些实际值，就会在同样路径结束。

符号执行的缺陷

如果代码包含递归或者循环，且终止条件符号化，可能会产生无数条路径（路径爆炸）。当符号路径约束包含了不能通过约束求解器求解的公式时，就不能得到输入值。

符号执行的挑战

symbolic_execution_challenge

解决方案

路径爆炸
宏观角度
- 限制符号执行次数
- 限制循环迭代次数
具体方法
- 启发式地优先探索当前最有效的路径
- 使用可靠的程序分析技术降低路径探索的复杂性
约束求解
提高约束求解器的能力，如不相关的约束消除、增量求解

华为案例:

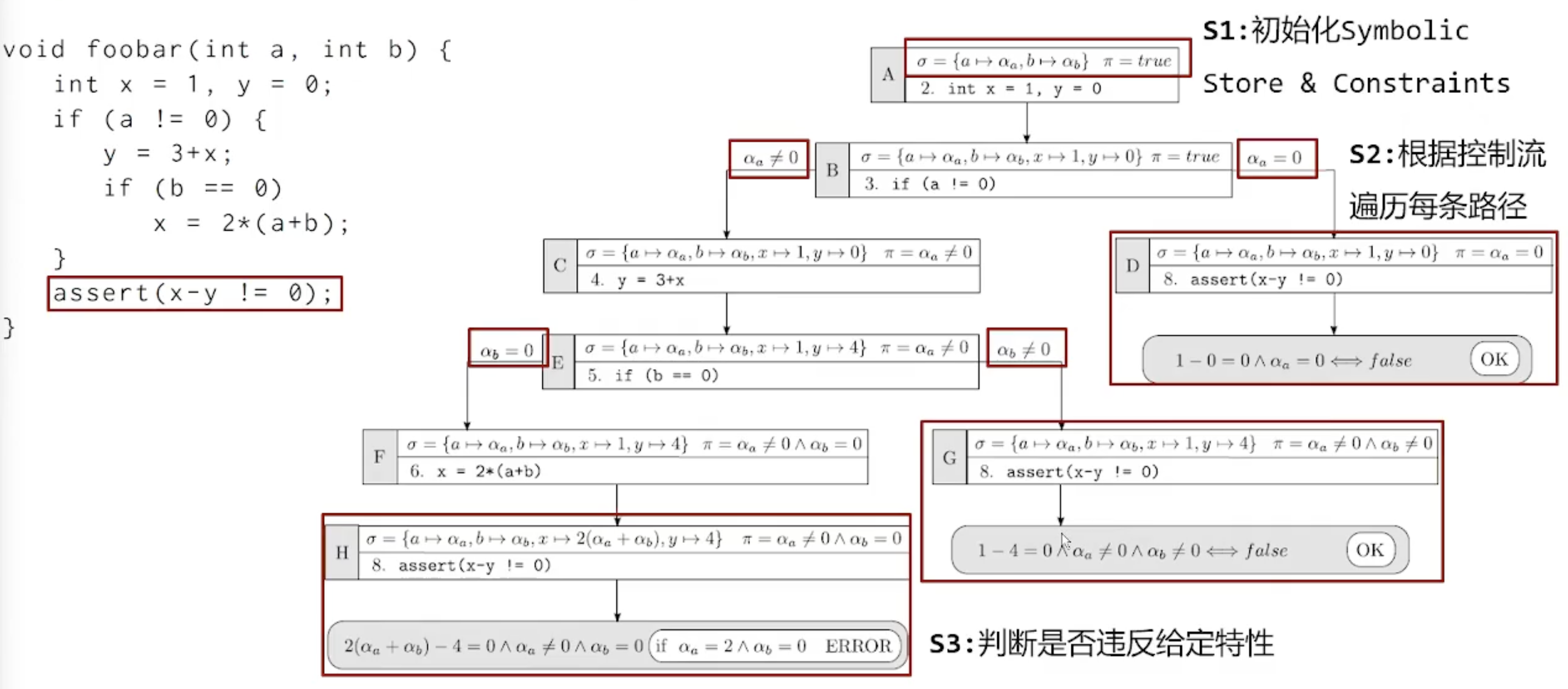
symbolic_execution_example

如图所示，每分析一条语句，就会更新 符号状态 σ 和 符号路径约束 PC（此处使用 π 代指），有些分支是显然不会违反给定特性的，如右上角，$1-0=0 \and α_a = 0$ 是不可能为 True 的，也就是不会违反给定特性（assert）。

而左下角的分支在 $α_a = 2 \and α_b = 0$时，就会违反特性。

污点分析¶

污点分析可以抽象成一个三元组<sources,sinks,sanitizers>的形式：

source：污点源，代表直接引入不受信任的数据或者机密数据到系统中;
sink：污点汇聚点，代表直接产生安全敏感操作(违反数据完整性)或者泄露隐私数据到外界(违反数据保密性);
sanitizer：无害处理，代表通过数据加密或者移除危害操作等手段使数据传播不再对软件系统的信息安全产生危害

污点分析就是分析程序中由污点源引入的数据是否能够不经无害处理，而直接传播到污点汇聚点。如果不能，说明系统是信息流安全的;否则，说明系统产生了隐私数据泄露或危险数据操作等安全问题。

（以 cflow 为例）通俗的理解就是，source，例如假设你想研究配置项漏洞，那么你就把配置项作为污点，将所有外部 API 作为 sink，通过污点分析，查看污点传播路径，例如 source -> f1 -> f2 -> sink 这是一条传播路径。

例子：

[...]
scanf("%d", &x);    // Source 点，输入数据被标记为污点信息，并且认为变量 x 是污染的
[...]
y = x + k;          // 如果二元操作的操作数是污染的，那么操作结果也是污染的，所以变量 y 也是污染的
[...]
x = 0;              // 如果一个被污染的变量被赋值为一个常数，那么认为它是未污染的，所以 x 转变成未污染的
[...]
while (i < y)       // Sink 点，如果规定循环的次数不能受程序输入的影响，那么需要检查 y 是否被污染

当然，污点不仅可以通过数据依赖传播，还可以通过控制依赖传播。

if (x > 0)
    y = 1;
else
    y = 0;

变量 y 的取值依赖于变量 x 的取值，如果变量 x 是污染的，那么变量 y 也应该是污染的。

https://www.bilibili.com/video/BV1Fq4y1B74m/ 1:11:00

模糊测试¶

模糊测试（fuzzing）是一种软件测试技术，其核心思想是将自动或半自动生成的随机数据输入到一个程序中，并监视程序异常，以发现可能的程序错误，比如内存泄露等。

黑盒 Fuzzing¶

Fuzzing 的目标是为了更快、更多地发现软件漏洞，其基本思路如下：

黑盒测试

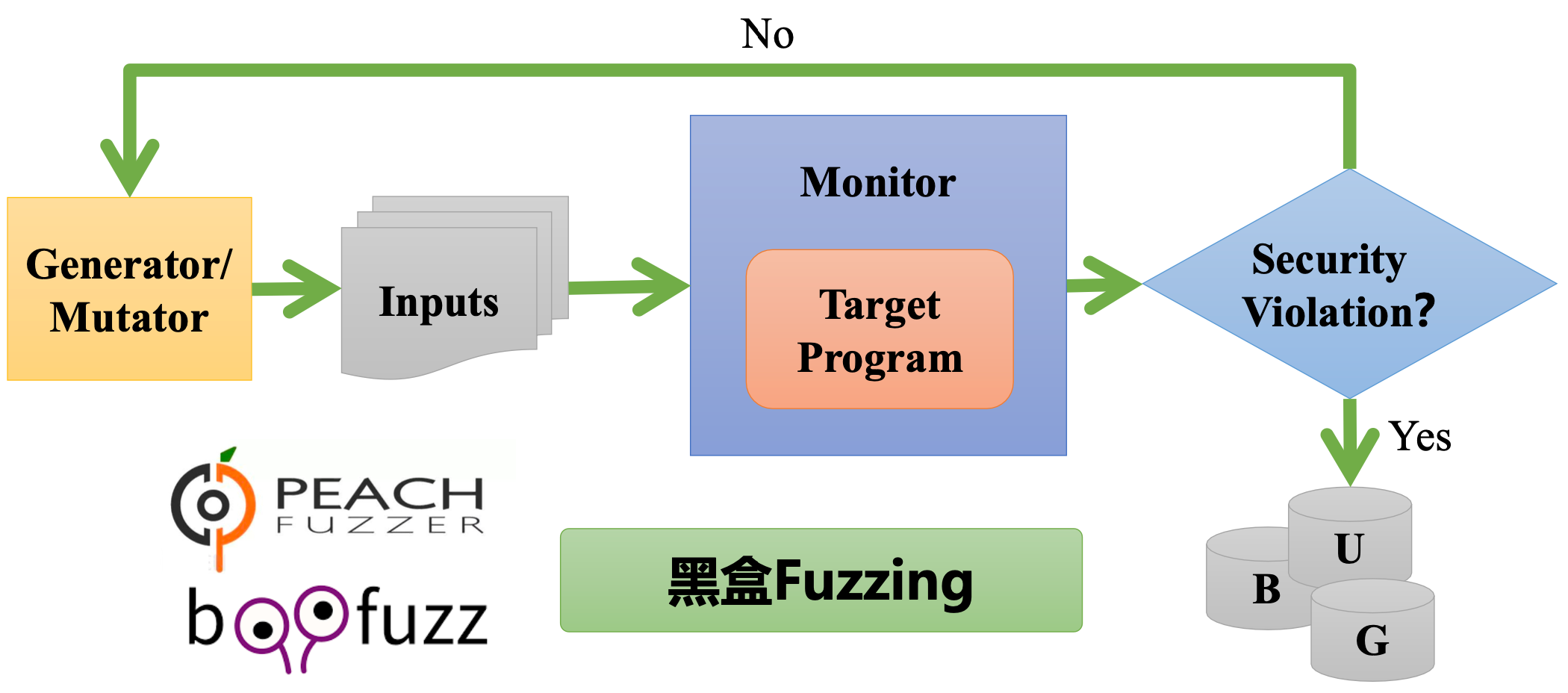
上述是黑盒 Fuzzing 的思路：

通过 Generator/Mutator 等生成策略生成输入，然后将其输入到目标程序中，存在一个 Monitor 监控，监控是否发生安全漏洞。
黑盒 Fuzzing 不关心程序执行的情况，而仅仅只是将程序作为黑盒，直接产生输入然后尝试找到结果。
因此，黑盒 Fuzzing 又被称为数据驱动的 Fuzzing，大部分传统的 Fuzzing 都是黑盒的。

与黑盒相对应的还有白盒 Fuzzing，白盒 Fuzz 在测试之前通常会先对应用进行分析，获取一定的信息来辅助其创建的输入能在应用程序中发现崩溃，符号执行 是白盒 Fuzzing 的常用技术。

黑盒 Fuzzing 由于只是机械的重复尝试输入，而输入又有无数种可能，因此效率低下。

灰盒 Fuzzing¶

在此引入现代 Fuzzing 的基本思想：遗传算法（Genetic Algorithm）+ 覆盖率（Coverage）统计。

覆盖率

覆盖率可大致分为三种：

Statement Coverage：语句覆盖率，即当前输入会覆盖（运行）多少条语句
Branch Coverage：分支覆盖率，即当前输入会覆盖（运行）多少个分支（if），if 语句无论为真还是假都算运行。
☆Edge Coverage：边覆盖率，基于 Control Flow Graph，是 AFL 运用的覆盖率，其原理如下图：

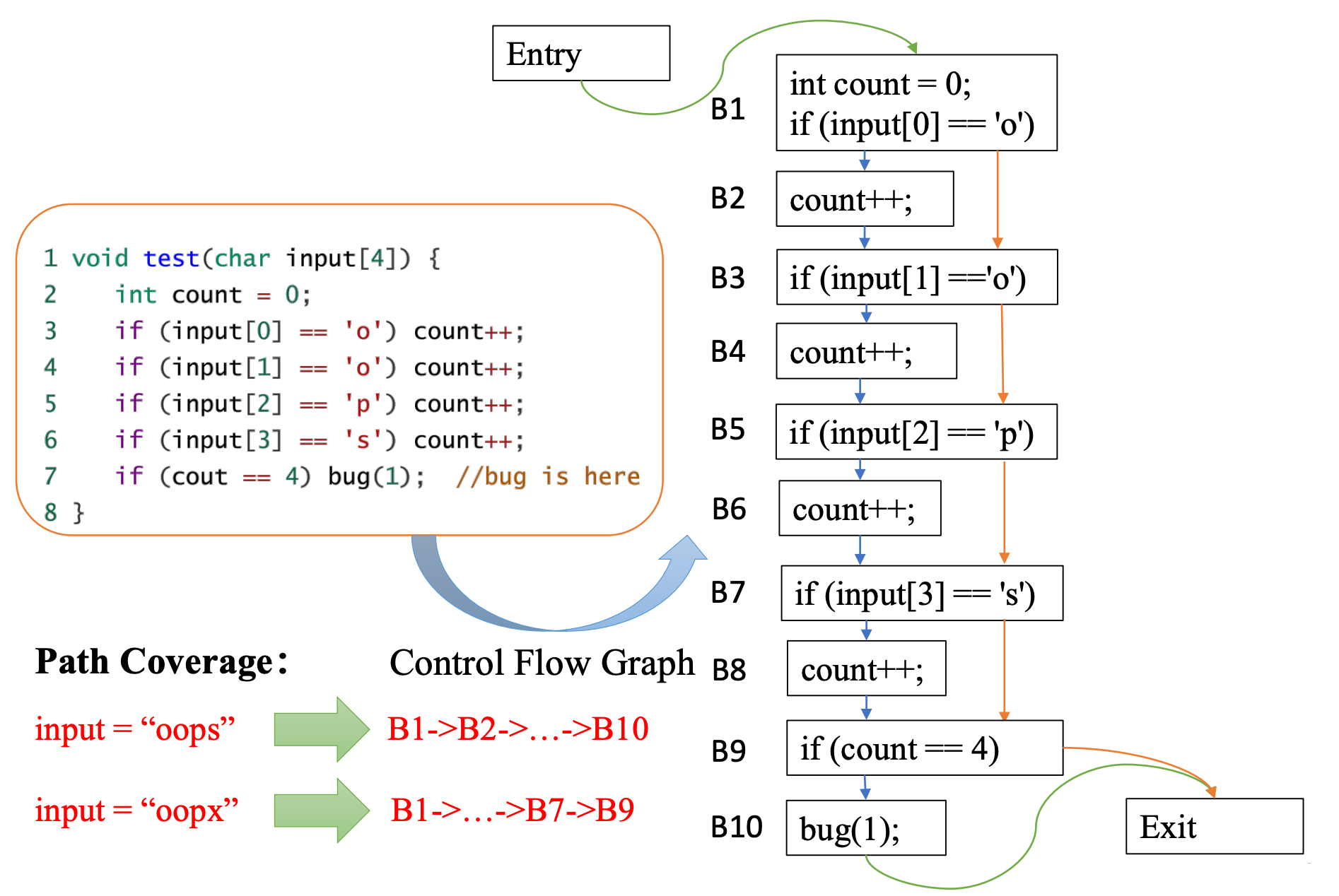
Edge Coverage

如图，左边是待测试源码，右边是控制流图。当input = "oops"时，其经过的控制流图的边为B1->B2->...->B10。

生成策略

简单介绍三种：

Mutation-Based Fuzz：一般会提供一个到多个有效的样本，基于变异 Fuzz 方式对这些样本进行变异。常用的方式有字节级跳变、块级别的替换、删除、增加、重复、基于字典的变异等。
Genertion-Based Fuzz：常使用的方法有基于随机字符的生成、基于语法结构的生成等。相对 Mutation-Based Fuzz，直接生成样本的方式覆盖率会更高。但是相对的，这种方式也需要更多的种子样本，对样本的依赖性也更强。
Hybrid Fuzz：考虑到 Genertion-Based 和 Mutation-Based 的优缺点，那么另一种方式就是结合两种模式共同进行 Fuzz，生成随机样本之后再进行相应的变换，以获得更好的 Fuzz 效率。

插桩

插桩技术指在保证原有程序逻辑完整性的基础上，在程序中插入探针，通过探针采集代码中的信息（方法本身、方法参数值、返回值等）在特定的位置插入代码段，从而收集程序运行时的动态上下文信息。

在 AFL 中，通过插桩，可以获知被测程序的运行信息（运行到那个路径），用来指导种子的变异提高模糊测试的效率。

灰盒 Fuzzing

灰盒 Fuzzing 的流程图如下：

白盒测试

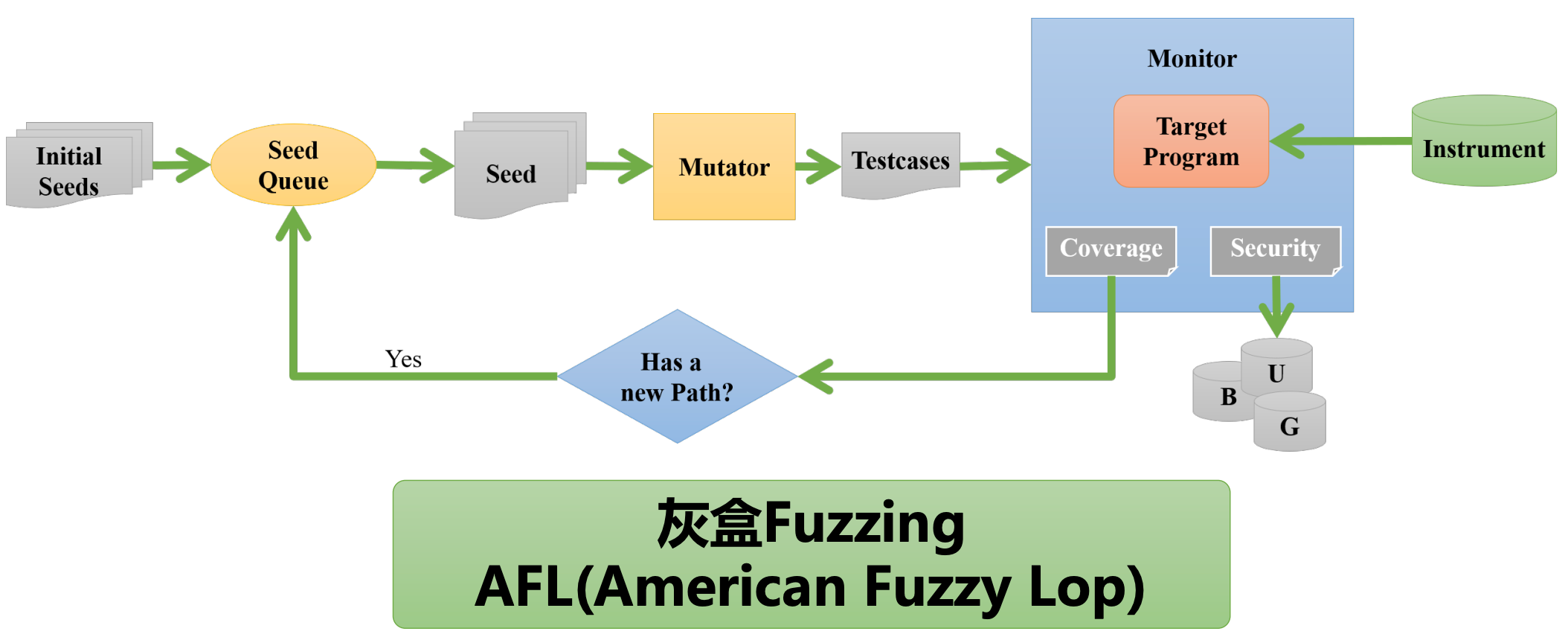
在黑盒 Fuzzing 的基础上做了如下改正：

不是直接生成测试样例，而是通过初始化种子。
如果该种子变异生成的测试样例产生了新的Path，就认为该种子是一个好种子，将其再次加入Seed Queue中。该思路就是 遗传算法 的思路。其中的Path指的是边覆盖率中的新路径。

上述方法是通过覆盖率的导向性策略，是 AFL 中使用的导向策略，随着机器学习的发展，逐渐引入了其他的覆盖率导向方法：基于随机下降算法的覆盖率导向方式、基于进化算法的覆盖率导向方式等来实现更高效的导向。

其他覆盖率策略如：Patch Based

总结

在灰盒 Fuzzing 中，学界主要研究如下四个方面的问题：

Seed Selection Strategy：种子选择策略
Seed Mutation Strategy：种子变异策略
Coverage Metrics：
Program Under Test：afl 主要用于 c，后续的研究将其扩展到了其他软件，如 java、linux kernel。

程序分析技术

基本概念¶

分析（analysis）与验证（verification）¶

编译器、AST、IR¶

编译器¶

AST¶

IR¶

IR 的生成、选择及应用方式¶

控制流图（CFG）与基础块（BB）¶

调用图（CG）与过程间控制流图（ICFG）¶

约束求解¶

SAT：布尔可满足性问题¶

SMT：可满足性模块理论¶

Z3 求解器¶

约束求解的应用¶

形式化验证¶

Boogie¶

Move Prover¶

其他¶

常用技术¶

数据流分析¶

指针分析¶

符号执行¶

污点分析¶

模糊测试¶

黑盒 Fuzzing¶

灰盒 Fuzzing¶

TODO¶

模型检测¶

基于模式的漏洞分析¶

二进制代码分析¶

程序分析技术

基本概念¶

分析（analysis）与验证（verification）¶

编译器、AST、IR¶

编译器¶

AST¶

IR¶

IR 的生成、选择及应用方式¶

控制流图（CFG）与基础块（BB）¶

调用图（CG） 与过程间控制流图（ICFG）¶

约束求解¶

SAT：布尔可满足性问题¶

SMT：可满足性模块理论¶

Z3 求解器¶

约束求解的应用¶

形式化验证¶

Boogie¶

Move Prover¶

其他¶

常用技术¶

数据流分析¶

指针分析¶

符号执行¶

污点分析¶

模糊测试¶

黑盒 Fuzzing¶

灰盒 Fuzzing¶

TODO¶

模型检测¶

基于模式的漏洞分析¶

二进制代码分析¶

调用图（CG）与过程间控制流图（ICFG）¶