南京大学《软件分析》

Reference from Static Program Analysis

Introduction¶

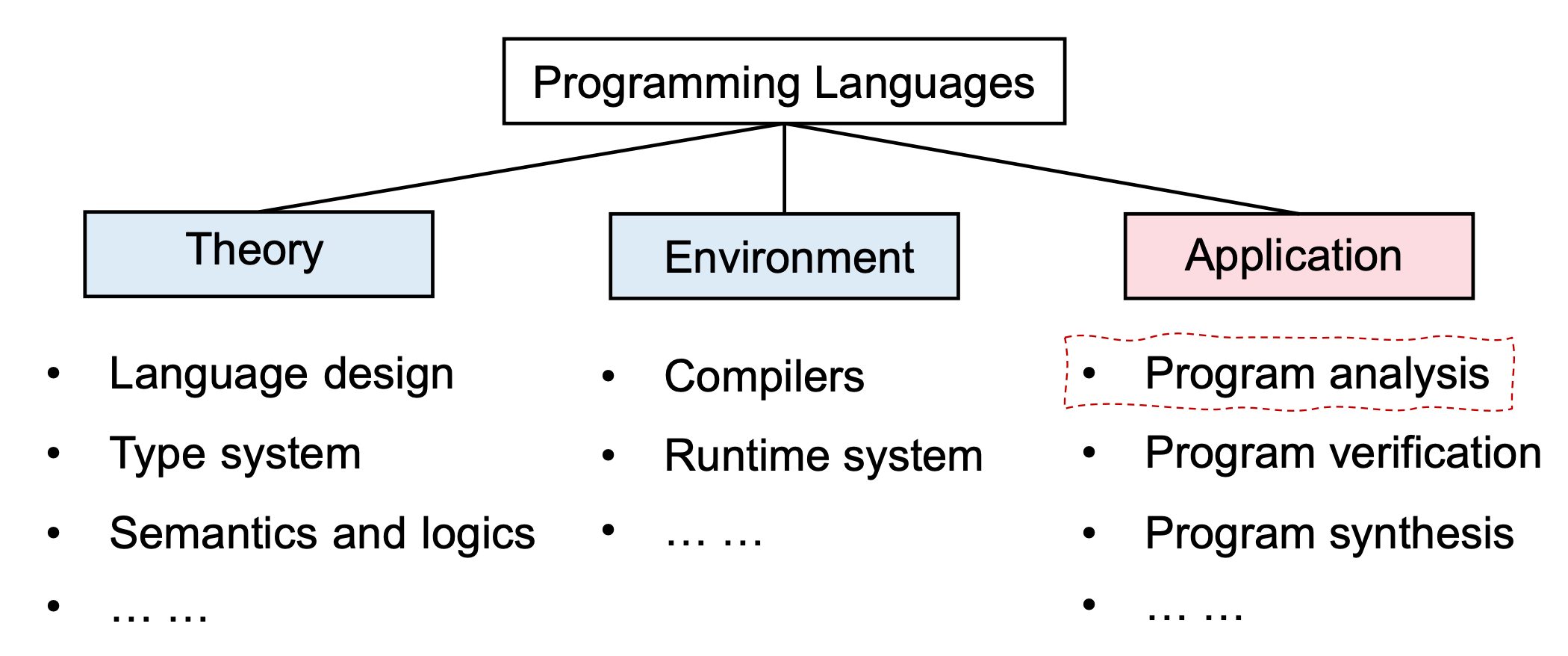
对于一个程序语言，可以大致理解为三个部分：

Theory：理论部分，包含程序的设计、语义逻辑等
Environment：运行所需的环境，编译器等
Application：程序的应用，为了保证所写程序的健壮性，需要对程序进行分析和验证！

Programming-Languages

在近十年的程序语言发展过程中，language cores 几乎没有变化，但是基于编程语言所编写的 program 越来越复杂。因此，如何保证复杂程序的可靠性、安全性、高效性呢？

静态程序分析是其中一种办法，它可以做到：

Program Reliability：Null pointer dereference, memory leak, etc.
Program Security：Private information leak, injection attack, etc.
Compiler Optimization：Dead code elimination, code motion, etc.
Program Understanding：
IDE call hierarchy：现代 IDE 通过静态分析，例如，可以实现当你鼠标放在变量名时，显示变量引用情况等功能
type indication

此外，学习静态程序分析，也可以帮助更深入地理解编程语言的语法、语义，自然而然地写出更可靠、更安全、更高效的程序。

静态分析通过分析程序 P 来推理其行为，并在运行程序 P 之前确定它是否满足某些属性（ properties），例如：

P 是否引用空指针？
P 中是否存在死代码？
P 中的 assert 断言会失败吗？
...

不幸的是，根据Rice's Theorem，目前没有办法明确的回答（Yes or No）程序是否满足no-trivial properties。

什么是no-trivial properties？

其定义较为复杂，可以近似理解为：the properties related with run-time behaviors of programs

因此，上述的三个问题都属于no-trivial properties，可以说，几乎所有值得我们感兴趣的问题都属于no-trivial properties！

如果一个静态分析，可以明确的回答程序是否满足no-trivial properties，那这个静态分析称为：Perfect static analysis，显然，Perfect static analysis是 不存在 的！

此处引入Sound和Complete的概念，一个Perfect static analysis是既Sound又Complete的，逻辑与的关系！

显然，二者只能得其一，满足其一的称为Useful static analysis：

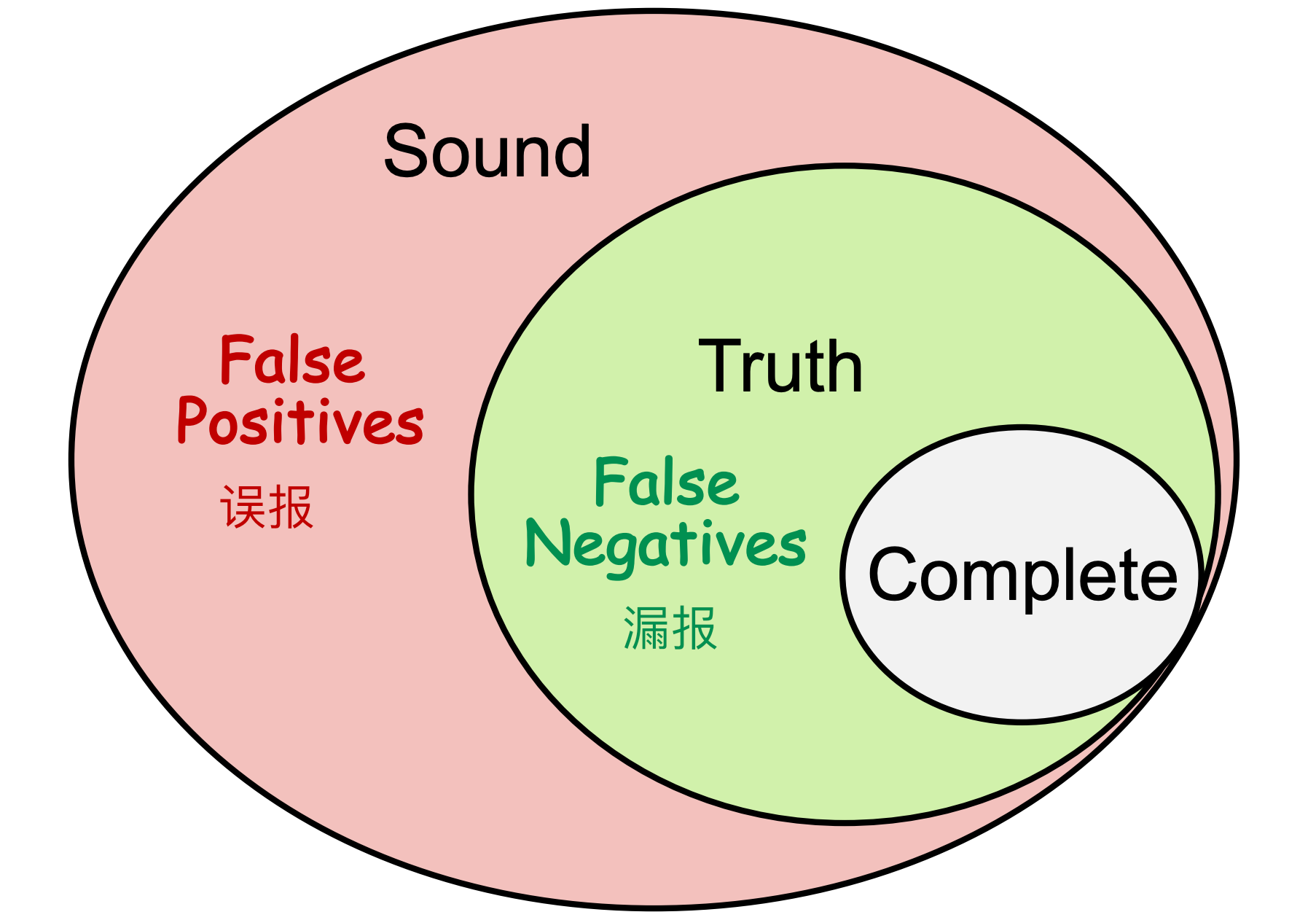
☆Compromise completeness -> sound (false positives)
让 completeness 妥协，即满足 sound 特性，不会漏报，只会误报，因此为 false positives。
Compromise soundness -> complete (false negatives)
让 soundness 妥协，即满足 complete 特性，不会误报，只会漏报，因此为 false negatives。

positives 的程序是有问题的程序（阳性），negatives 的程序是良好的程序（阴性）。

false positives，即假阳性，把良好的程序误报为有问题的程序。

false negatives，即假阴性，把有问题的程序漏报了，认为其没问题！

注意：大多数情况下，会选择Compromise completeness，即选择满足Sound。

Soundness 的必要性： 如果一个静态分析是Sound的，那它就能够识别出一切有问题的程序，不会出现漏报。但如果一个静态分析是Complete的，那它一定能接收（验证通过）良好的程序，即不会出现误报。但是，Complete的静态分析，会导致漏报，一但静态分析通过了错误的程序，那么该错误就无法被修复，导致运行时的错误！

Sound-Complete

两个单词总结静态分析：

Abstraction
Over-approximation
Transfer functions
Control flows

中间表示¶

Intermediate Representation

Compilers and Static Analyzers¶

编译器分为前端和后端，前端负责将源码编译为中间表示，后端负责将中间表示编译为机器代码，具体流程如下：

Scanner，词法分析器，接受源码输出字符流。
Parser，语法分析器，接受字符流，输出 AST
Type Checker：语义分析器，进行类型检查等工作，输出也是 AST
Translator：编译器中端将 AST 翻译为多种中间表示（IR），常用的如三地址码。静态分析通常基于 IR 进行！
Code Generator：编译器后端将 IR 翻译为机器代码

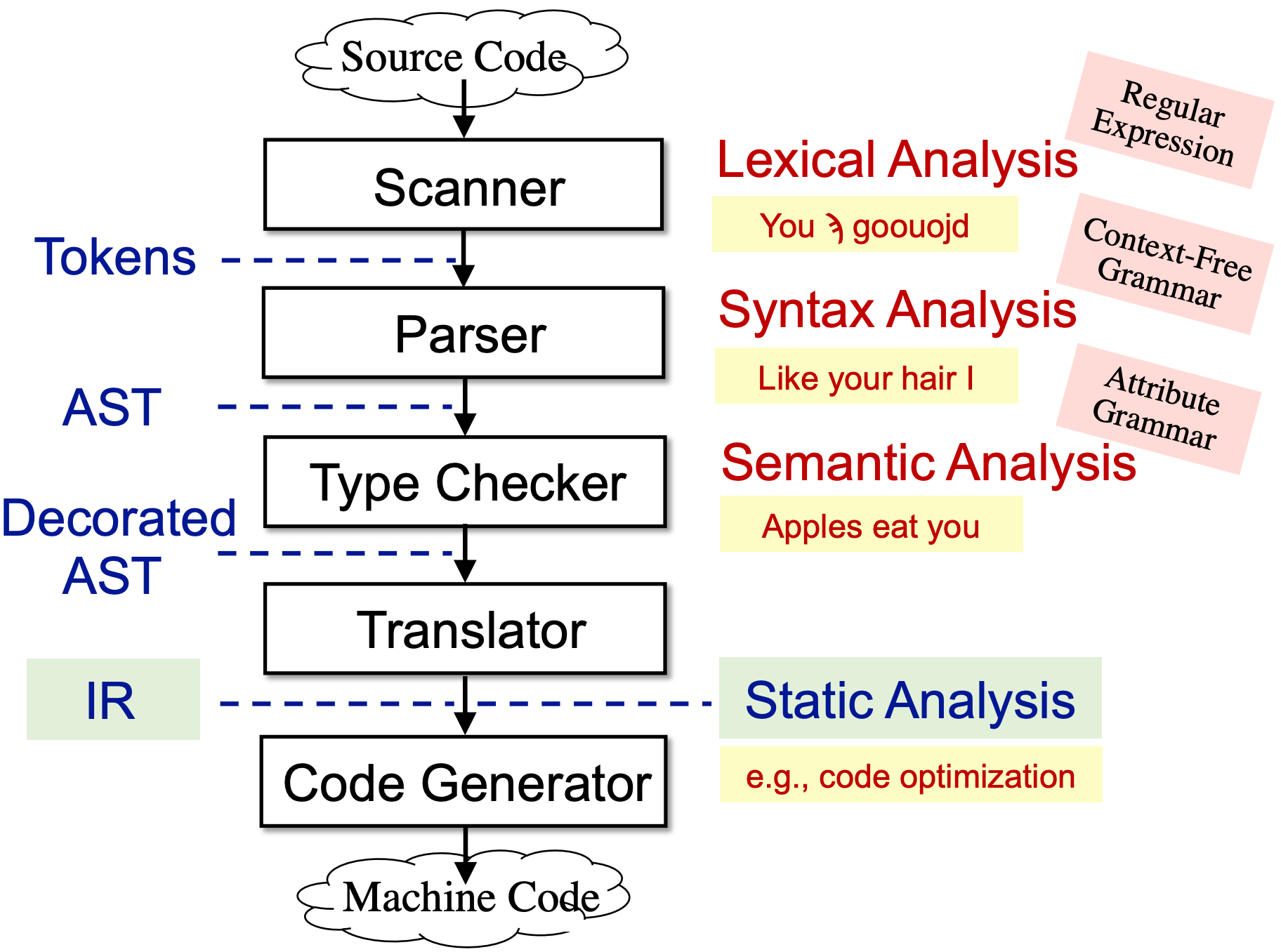
Compilers-and-Static-Analyzers

也就是说，想要进行静态分析，必须先使用编译器前端将源代码翻译为 IR。

若将编译器分为前端和后端，则前端为生成 IR 前的部分，后端为基于 IR 生成目标代码（e.g. 机器码）的部分。

AST vs. IR¶

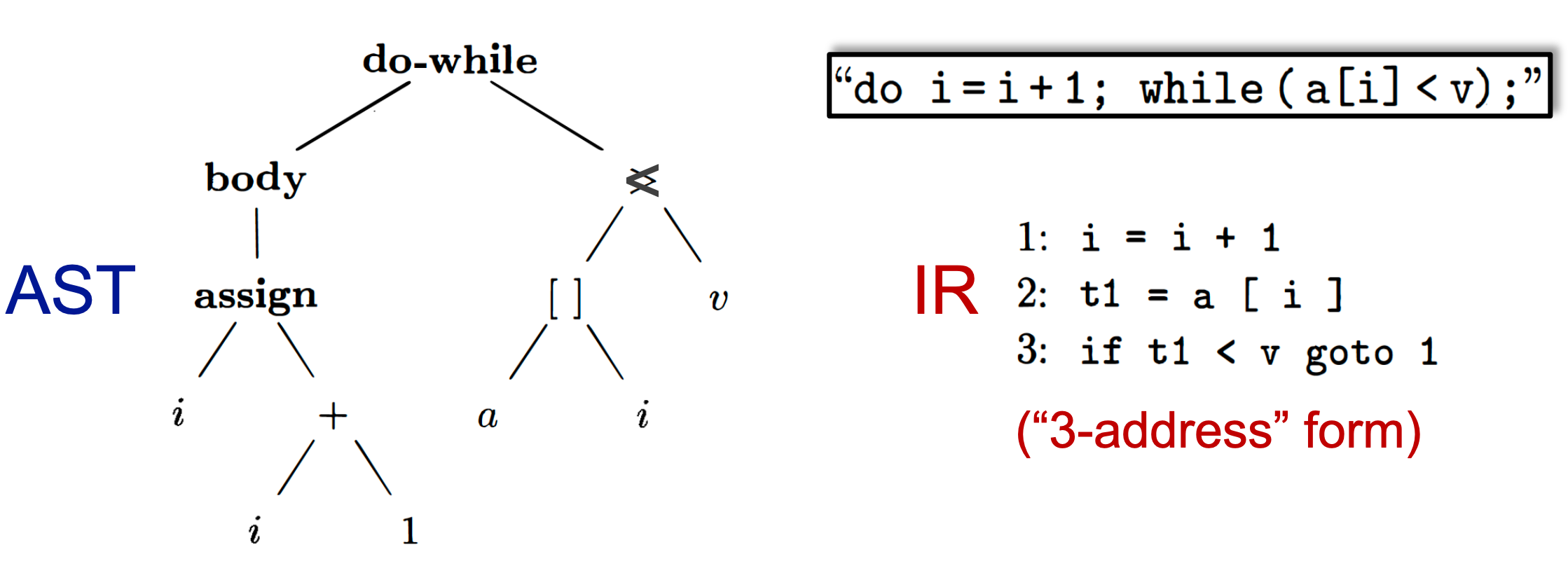
AST-IR

AST

high-level，更接近程序结构
依赖源程序语言
suitable for fast type checking
缺少 control flow 信息

IR

low-level，更接近机器代码
独立于源程序语言
compact and uniform
包含 control flow 信息
usually considered as the basis for static analysis

IR: Three-Address Code (3AC)¶

三地址码指令的右侧最多只能有 1 个运算符。

t2 = a + b + 3

// 转化为三地址码
t1 = a + b
t2 = t1 + 3

Address can be one of the following：

Name：a, b
Constant：3
Compiler-generated temporary: t1, t2

3AC 常见的格式：

x = y bop z
x = uop y
x = y
goto L
if x goto L
if x rop y goto L

// description
x, y, z: addresses
bop: binary arithmetic or logical operation       // 二元运算符/逻辑运算符
uop: unary operation (minus, negation, casting)   // 一元运算符
L: a label to represent a program location        // 代表程序位置的表示符
rop: relational operator (>, <, ==, >=, <=, etc.) // 比较运算符
goto L: unconditional jump                        // 无条件跳转
if … goto L: conditional jump                     // 有条件跳转

3AC in Real Static Analyzer: Jimple¶

Soot 是目前最流行的 Java 静态分析框架，Soot 的 IR 是 Jimple：typed 3-address code

Jimple 中常用的概念解析：

invokespecial：call constructor, call superclass methods, call private methods
invodevirutal：call instance methods (virtual dispatch)，也就是常用方法调用，调用实例的方法
invokeinterface：cannot optimization, checking interface implementation，调接口的方法
invokestatic：call static methods
invokedynamic（Java 7)：Java static typing, dynamic language runs on JVM
method signature：即方法签名，其格式为 calss_name: return_type method_name(parameter1_type, ...)
Jimple 中的 clinit 方法：将变量、类装入内存中，并初始化

package nju.sa.examples;
public class Class3AC{
    public static final double pi = 3.14;
    public static void main(String[] args){

    }
}

此时被翻译成三地址码 Jimple 如下：

public class nju.sa.examples.Class3AC extend java.lang.Object{ // Object 是所有类的基类
    public static final double pi;
    public void<init>(){...}  // 调用默认的初始化方法
    public static void main(java.lang.String[]){...}
    // 初始化静态变量 pi
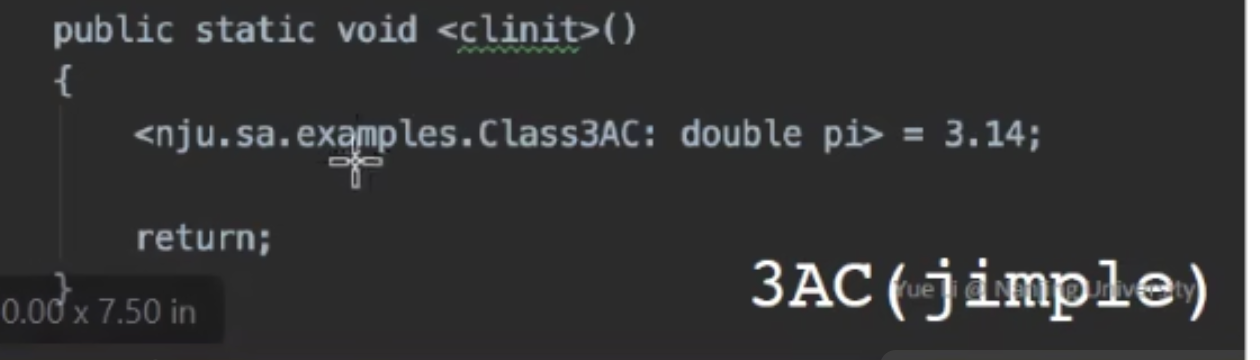
    public static void <clinit>(){
        <nju.sa.examples.Class3AC: double pi> = 3.14;
        return;
    }
}

StringBuilder-IR

调用$r3 的 append 方法，其余内容是该方法的 method signature（签名），依次是：

该方法来自哪个类
返回值类型
方法名
方法参数的类型
真正调用的参数是 r1

clinit-example

Todo：例子代码后续用 soot 生成后补充！参见PDF

Static Single Assignment（SSA）¶

SSA，即静态单赋值，其中所有的变量都有独一无二的名字：

每次定义时，给一个新名称
将新的名称传播到后续的使用中
每个变量都只会定义一次

## 3AC
p = a + b
q = p - c
p = q * d
p = e - p
q = p + q

将其修改为 SSA

## SSA
p1 = a + b
q1 = p1 - c
p2 = q1 * d
p3 = e - p2
q2 = p3 + q1

如果一个变量在控制流中 merge 了怎么办？

if e:
    x0 = 0
else:
    x1 = 1
y = x + 7 ## 此时，这个 x 应该如何命名？

SSA 引入一个特殊的 merge 操作符： Φ，称为 fhi-function。

于是，上述代码修改为：

...
x2 = Φ(x0,x1)
y = x2 + 7

SSA 的优点？

流信息被间接的合并到了变量名称中，在进行 flow-insensitive 分析时，可能可以得到 flow-sensitive 分析的精度
定义和使用对是显式的

在一些按需任务中支持更有效的数据事实存储和传播

一些优化任务在 SSA 上执行得更好(例如，条件常数传播，全局值编号)。

SSA 的缺点？

可能引入过多的变量和 phi-functions
在翻译到机器码时可能存在效率低的问题

控制流图（CFG, Control Flow Graphs）¶

CFG 是静态分析的基本结构，CFG 中的节点可以是一个单独的三地址码，也可以（通常）是一个基本块（BB）。

基本块是满足下列关系的三地址码的最大序列集合：

It can be entered only at the beginning, i.e., the first instruction in the block。只可以从 BB 中的第一条指令进入。
It can be exited only at the end, i.e., the last instruction in the block。只可以从 BB 中的最后一条指令退出。

How to build Basic Blocks？

输入：A sequence of three-address instructions of P
输出：A list of basic blocks of P
构建方法
找到 P 中区块的 leader（区块的首个指令）
- P 中的第一个指令是 leader
- 跳转指令（conditional or unconditional jump）的目标指令也是 leader（若他不单独作为 leader，则其所属 BB 将会有两个入口）
- 跳转指令的下一条指令也是 leader。因为假设你将跳转指令和它的下一条指令放在同一个 BB 中，此时该 BB 就有了两个出口。
Build BBs for P
- 一个 BB 包含一个 leader 和下一个 leader 之间的所有指令

INPUT

(1) x = input
(2) y = x - 1
(3) z = x * y
(4) if z < x goto (7)
(5) p = x / y
(6) q = p + y
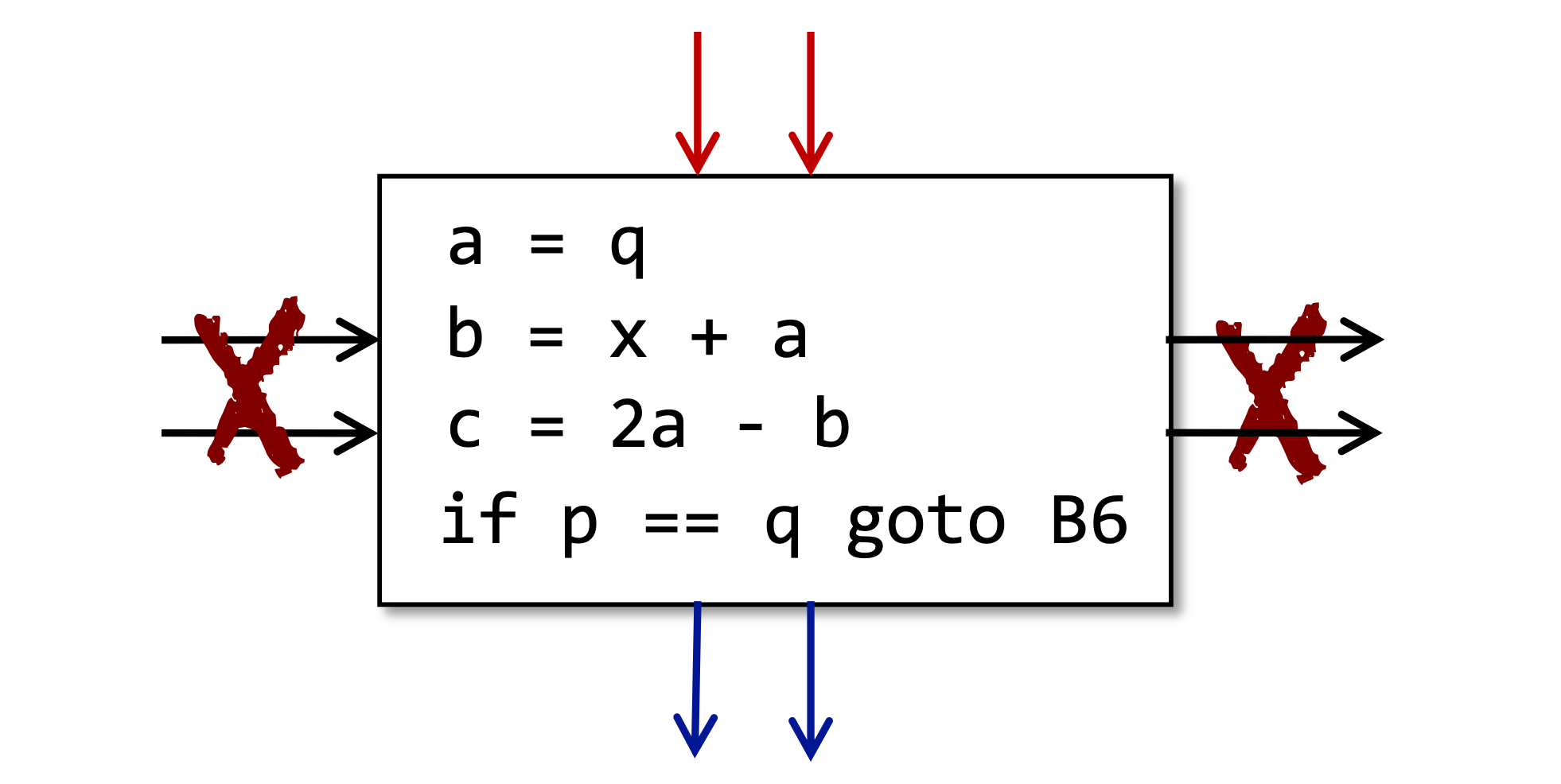
(7) a = q
(8) b = x + a
(9) c = 2a - b
(10) if p == q goto (12)
(11) goto (3)
(12) return

（1）Determine the leaders in P

P 中的第一个指令是 leader：{1}
跳转指令的目标指令也是 leader：{3, 7, 12}
跳转指令指令的下一条指令也是 leader：{5, 11, 12}
汇总 leaders = {1, 3, 5, 7, 11, 12}

（2）Build BBs for P

B1 {(1),(2)}
B2 {(3),(4)}
B3 {(5),(6)}
B4 {(7),(8),(9),(10)}
B5 {(11)}
B6 {(12)}

OUTPUT

OUTPUT

How to build Control Flow Graph？

CFG 的节点是 BB
当满足下列条件时，连接 block A 和 block B：
在 block A 的结尾存在跳转指令（conditional or unconditional jump），其跳转目标为 block B 的起始指令
顺序执行时，block B 的指令就在 block A 后面，且 block A 不以无条件跳转指令结束。

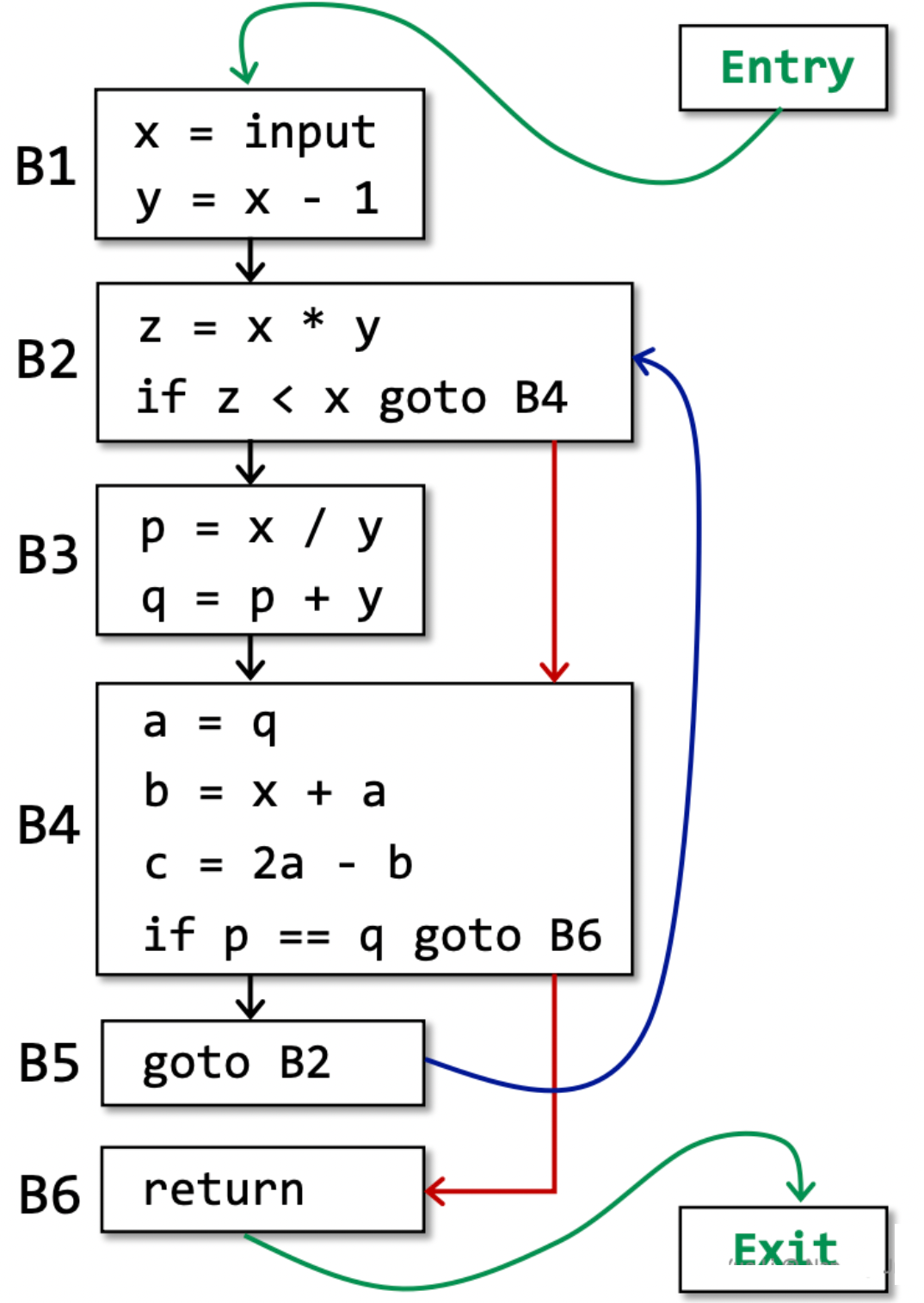
cfg-build

通常还会添加两个节点：Entry 和 Exit，目的是为了方便静态分析算法的设计。

从 Entry 到 BB 的一条边，包含 IR 的第一条指令
从任何包含一条指令的 BB 中退出的边缘，该指令可能是 IR 的最后一条指令

此外，通常还会将跳转指令的目标从指令标识符修改为区块标识符：

## block A
(j) goto (i)
## 修改为 goto B

## block B
(i) xxx

数据流分析¶

Overview of Data Flow Analysis¶

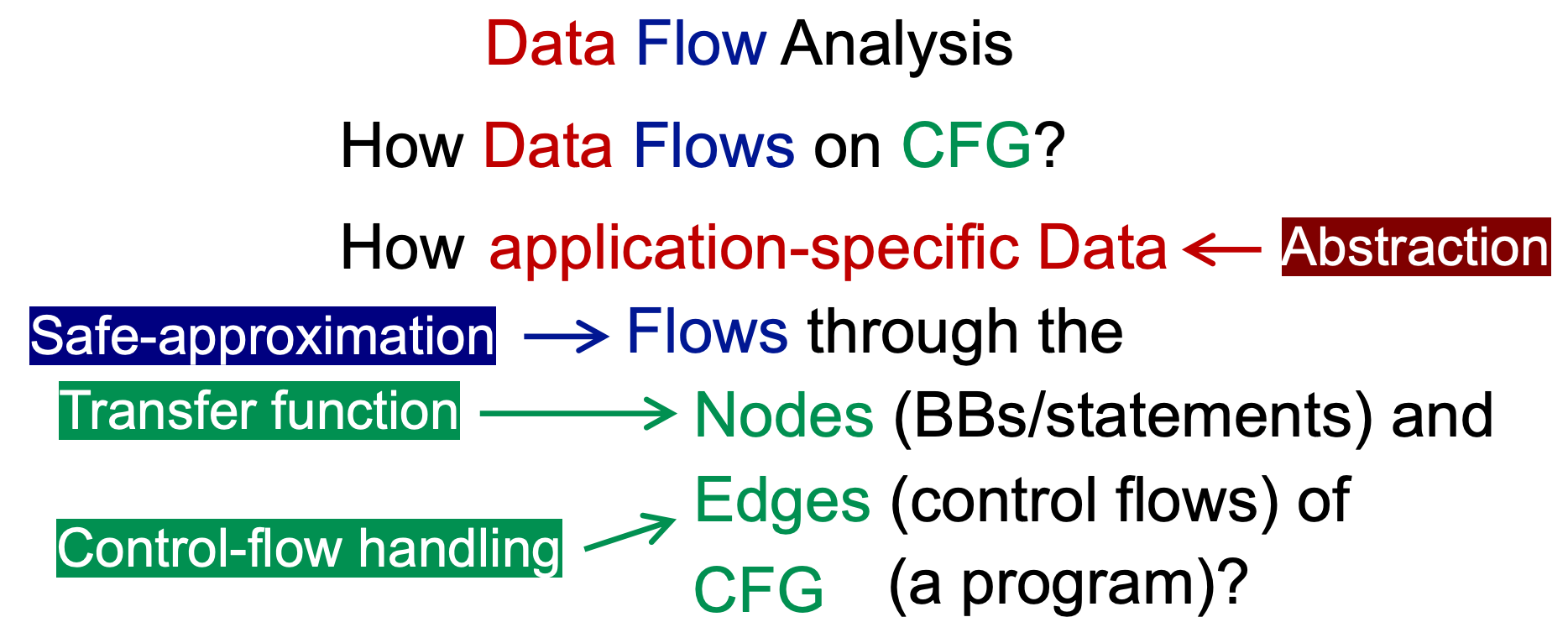
Data Flow Analysis，可以理解为：How Data Flows on CFG?

在此之前，曾用两个词总结了静态分析：

Abstraction
Over-approximation
Transfer functions
Control flows

其中 Abstraction 的部分就是将 Data 进行抽象，例如将数字类型抽象为 + - 0 T ⊥

对于绝大多数的静态分析，都采用 Over-approximation，但是仍有少数的情况下，需要采用 under-approximation。二者都是为了分析的安全性，因此统称为 Safe-approximation，应根据具体情况具体分析使用 Over or Under。

may analysis: 输出的结果 may be true，也就是可以误报，不许漏报（over-approximation）。并集 ∪

must analysis: 输出的结果 must be true，也就是可以漏报，不许误报（under-approximation）。交集 ∩

Transfer function 用于将 BB 中的内容转化为抽象的数据，例如正正得负 + op + = +

Control flows 是抽象数据的流动，以及在两条流汇聚的时候如何做处理？做交集或并集处理。

不同的 数据流分析应用 具有：① 不同的 data abstraction ② 不同的 Safe-approximation 策略（under/Over） ③ 不同的 transfer function ④ 不同的 control flows

Data-Flow-Analysis

Preliminaries of Data Flow Analysis¶

讲述数据流分析的前置知识。

每次 IR statement 的执行，都会将输入状态转换为新的输出状态。输入和输出状态与 IR statement 前后的 program point 相关联。

程序流的执行有如下三种方式：

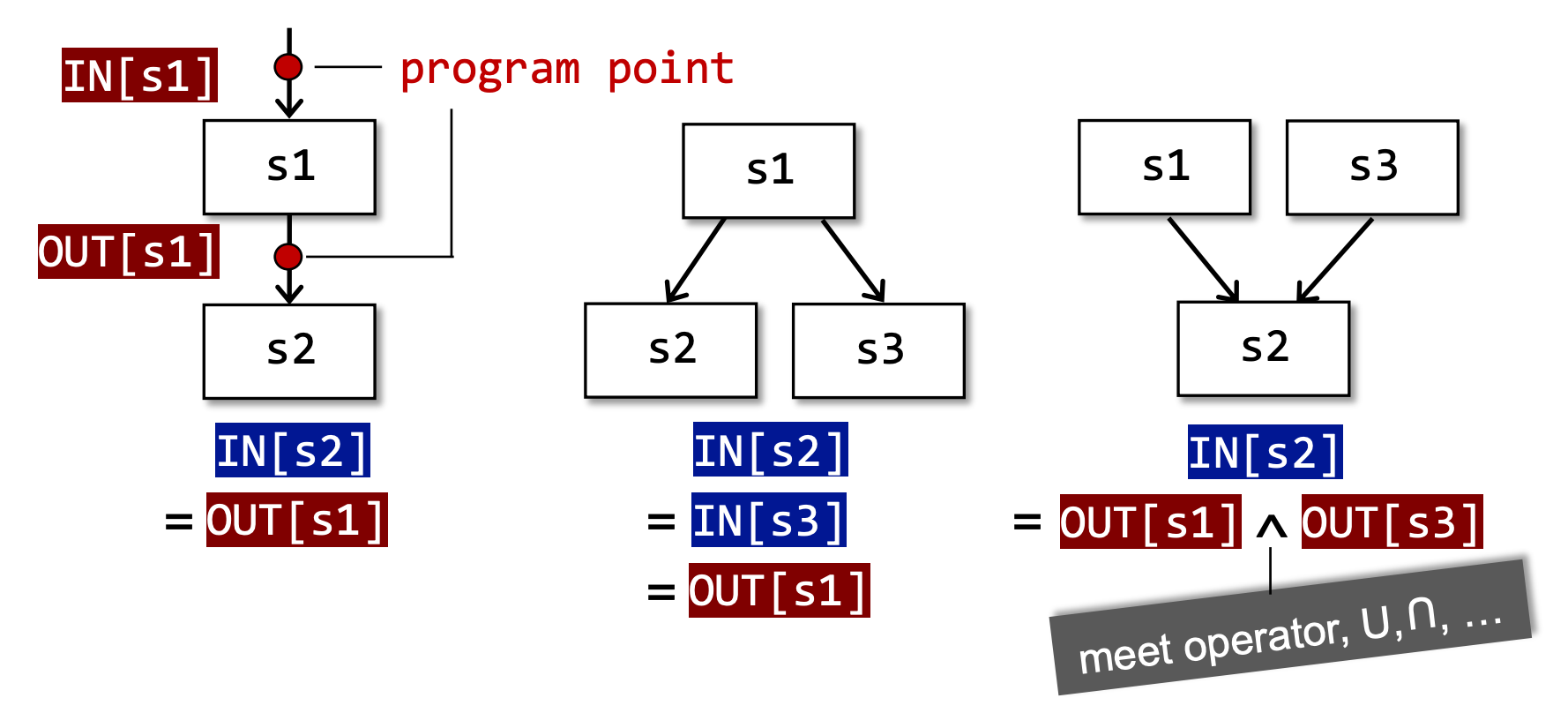
in-out

将 BB 或者 IR statement 的输入称为 IN[...] ，输出称为 OUT[...]

在第三种情况中，根据 may analysis和must analysis的不同，meet operator 分别为 ∪和∩。如果是may analysis就必须保证不漏报，因此取并集∪；而must analysis必须保证不误报，因此取交集∩。

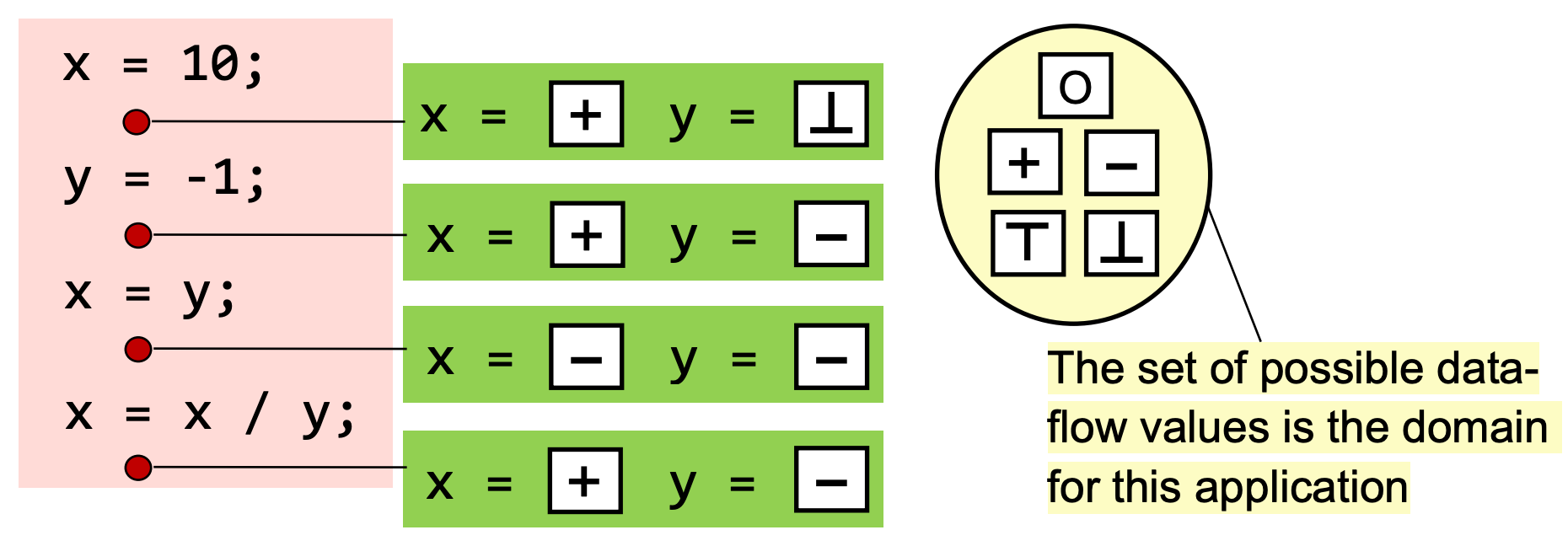
point-value-domain

在每个数据流分析应用程序中，我们将每个 program point 与一个 data-flow value 相关联，该值表示对该点可观察到的所有可能的 program states set 的 Abstraction。

所有可能的 data-flow value 的集合称为 Domain。

Data-flow analysis is to find a solution to a set of safe-approximationdirected constraints on the IN[s]’s and OUT[s]’s, for all statements s.

constraints based on semantics of statements (transfer functions)
constraints based on the flows of control

数据流分析分为 Forward Analysis 和 Backward Analysis，其符号表示如下：

Notations-for-Transfer-Function’s-Constraints

注：有些人在进行 Backward Analysis 时，将 CFG 反向建立，然后再对反向 CFG 进行 Forward Analysis，以达到 Backward Analysis 的效果。

以 Forward Analysis 为例，f_s 的输入是 IR statement 。s 的输入 IN[s]，输出是 OUT[s]。

可以理解为，在s运行完之后，其输出为 OUT[s]。至于什么是 OUT[s]，下文详解。

上述的例子都是以 IR statement 为例，在实际分析中，IR 往往是指 CFG，因此数据流分析的 Node 应该是 BB，其符号定义如下：

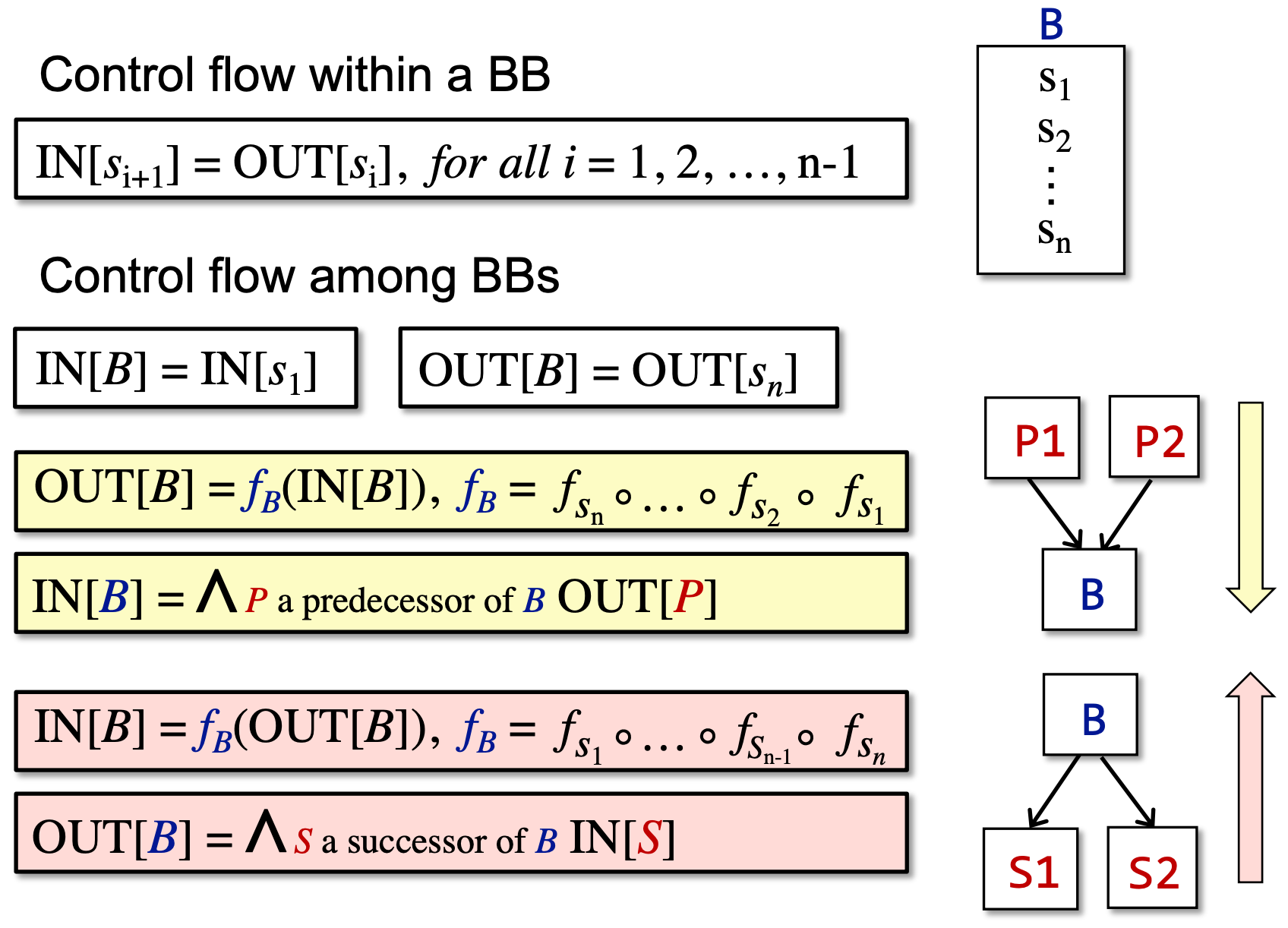
Notations-for-Control-Flow’s-Constraints2

meet operator ∧ 用于汇总不同路径的结果，往往是做交集∩或并集 ∪处理。

在上述的理论基础下，对三种 Data Flow Analysis Applications 进行介绍，但不涉及如下内容：

Method Calls，方法调用，过于复杂，在 Inter-procedural Analysis 中讲解
Aliases，讲述的例子都没有 Aliases，将在 Pointer Analysis 中讲解

Applications¶

Reaching Definitions Analysis¶

Definitions

A definition d at program point p reaches a point q if there is a path from p to q such that d is not “killed” along that path

在 program point p 存在一个 definition d，例如 v = 1，如果在 p-> q 的这条路径上不存在变量 v 的新的赋值定义，那就说明这个 definiteion d 没有被杀死，是可以到达的。

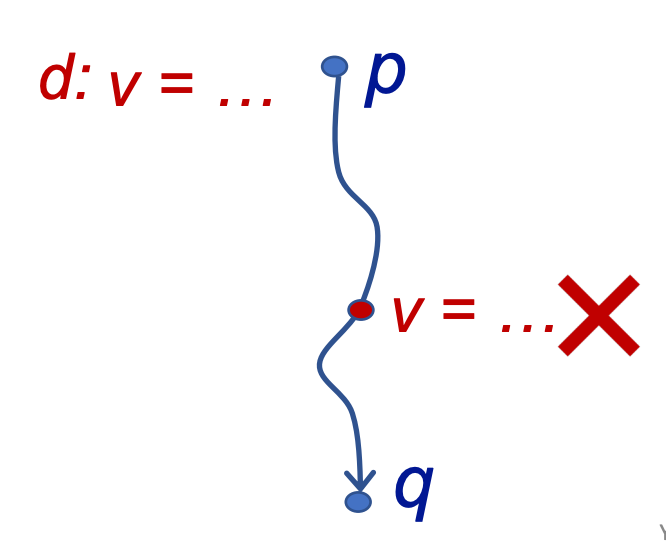
reaching-definitions-analysis-example

Usage

到达定义分析可以用于检测潜在的 undefined variables。

例如，在 CFG 的 Entry 节点引入所有变量的虚拟定义（dummy definition），如果其中一个虚拟定义 v 到达了一个 program point p，根据到达分析的定义，说明 Entry 和 p 之间，没有重新赋值定义变量 v，如果 p 使用了变量 v，说明他使用的是未定义的变量 v。

Abstraction

Data Flow Values/Facts：

The definitions of all the variables in a program
Can be represented by bit vectors（常用的表达形式）
e.g., D1, D2, D3, D4, …, D8 (8 definitions)
使用比特表示：00000000，0 表示不可达，1 表示可到达

Safe-approximation

Transfer Function：OUT[B] = gen_B U (IN[B] - kill_B)
gen_B是 BB 中的所有定义语句 D
IN[B]顾名思义，等于上一个 BB 的 OUT
kill_B是指，如果当前 BB 中重新定义了变量 v，那么就要删除所有其他对于变量 v 的定义。删除是指，将对应定义 D_i的比特置为 0
Control Flow：IN[B] = U_{P a predecessor of B} OUT[P]
该算法采用 may analysis，因此如果遇到分支汇合的情况，取所有分支的并集∪。
该算法采用 forwards direction

Algorithm

INPUT: CFG (kill_B and gen_B computed for each basic block B)

OUTPUT: IN[B] and OUT[B] for each basic block B

算法如下：

OUT[entry] = ∅;
for (each basic block B\entry){
  OUT[B] = ∅;
}
while (changes to any OUT occur){            // 当 OUT 发生改变时，继续循环
  for (each basic block B\entry) {           // 遍历所有节点
    IN[B] = UP a predecessor of B OUT[P];    // 即 Control Flow，所有上流分支的并集作为该BB的输入
    OUT[B] = genB U (IN[B] - killB);         // 即 Transfer Function
    }
}

B\entry是指排除 Entry 这个节点，在上述算法中，其实没有必要分开，因为都是初始化为∅，但是如果算法采用 must analysis时，for 循环内不是初始化为空，后续会谈到。但由于这个算法是一个经典的模板，因此设计的时候尽可能通用。

该循环为什么会终止？

gen_B和 kill_B固定不会发生变化
唯一发生变化的是 OUT，但是 Data Flow Values 一旦被加入 OUT 之后，会永远保留。即 OUT 只能 0→1 或者 1→1，不可能 x→ 0。此外，值得注意的是，IN 不变化时，OUT 也不会变化。
由于 Data Flow Values 是有限的，因此最终 OUT 也不会变化，循环因此停止。

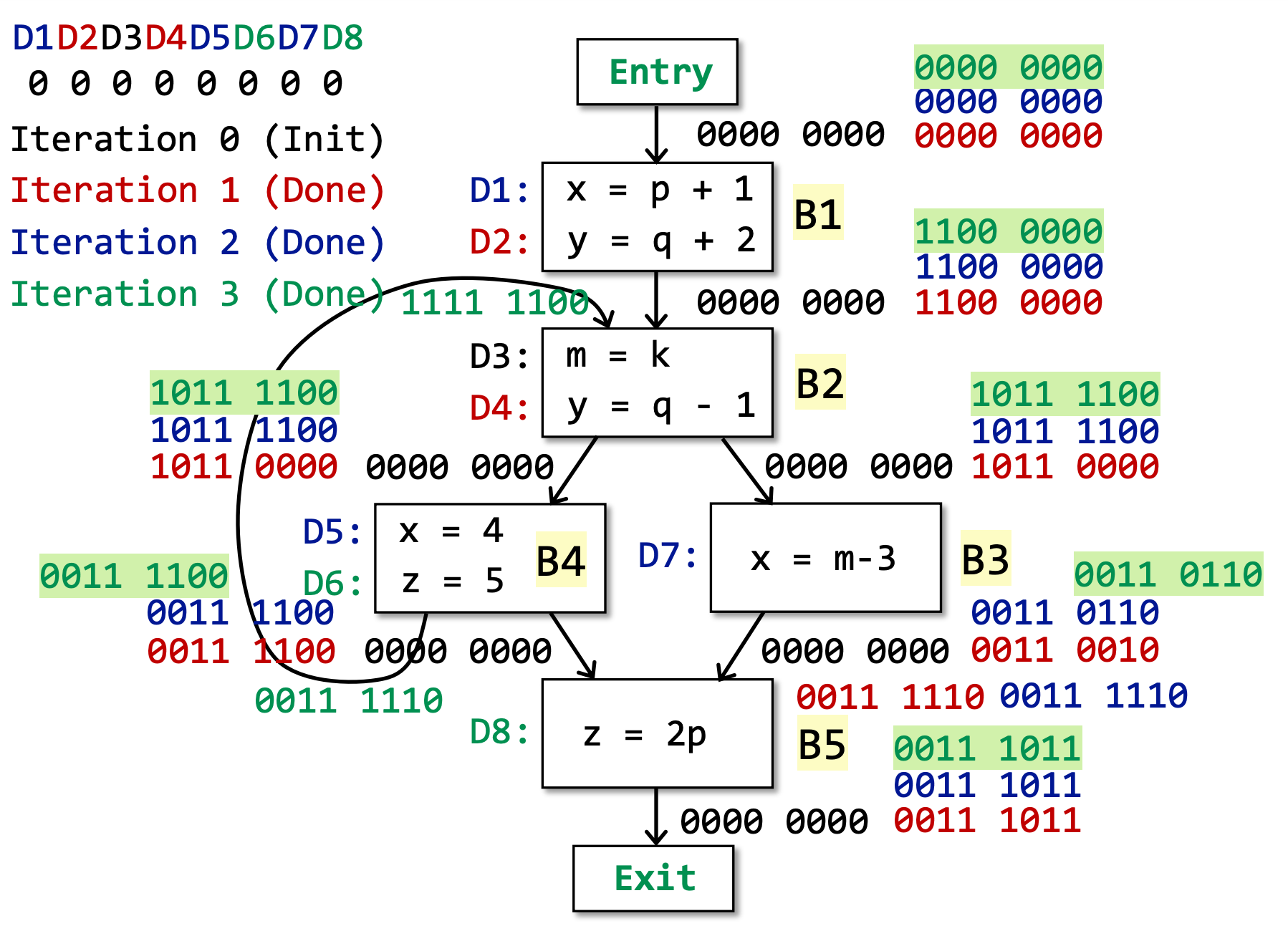
Reaching-Definitions-Analysis-Example

TODO: 解释

Live Variables Analysis¶

Definitions

如果 程序点 p 处的 变量 v 可以在 CFG 图中，以 p 为起始点的某条路径中被使用，则称其在 程序点 p 上 live，否则为 dead。且如果 变量 v 在被使用之前被重定义了，那也认为其为 dead

live-variables-analysis-example

Usage

Live variables 的分析结果可以用于寄存器分配。

例如，在某个时刻，所有寄存器都满了，我们需要使用一个寄存器，因此需要删去其中一个寄存器的内容，此时应该删去存放 dead variables 的寄存器。

Abstraction

Data Flow Values/Facts：

All the variables in a program
Can be represented by bit vectors
e.g., V1, V2, V3, V4, …, V8 (8 definitions)
使用比特表示：00000000，0 表示该变量 Dead，1 表示该变量 Live

Safe-approximation

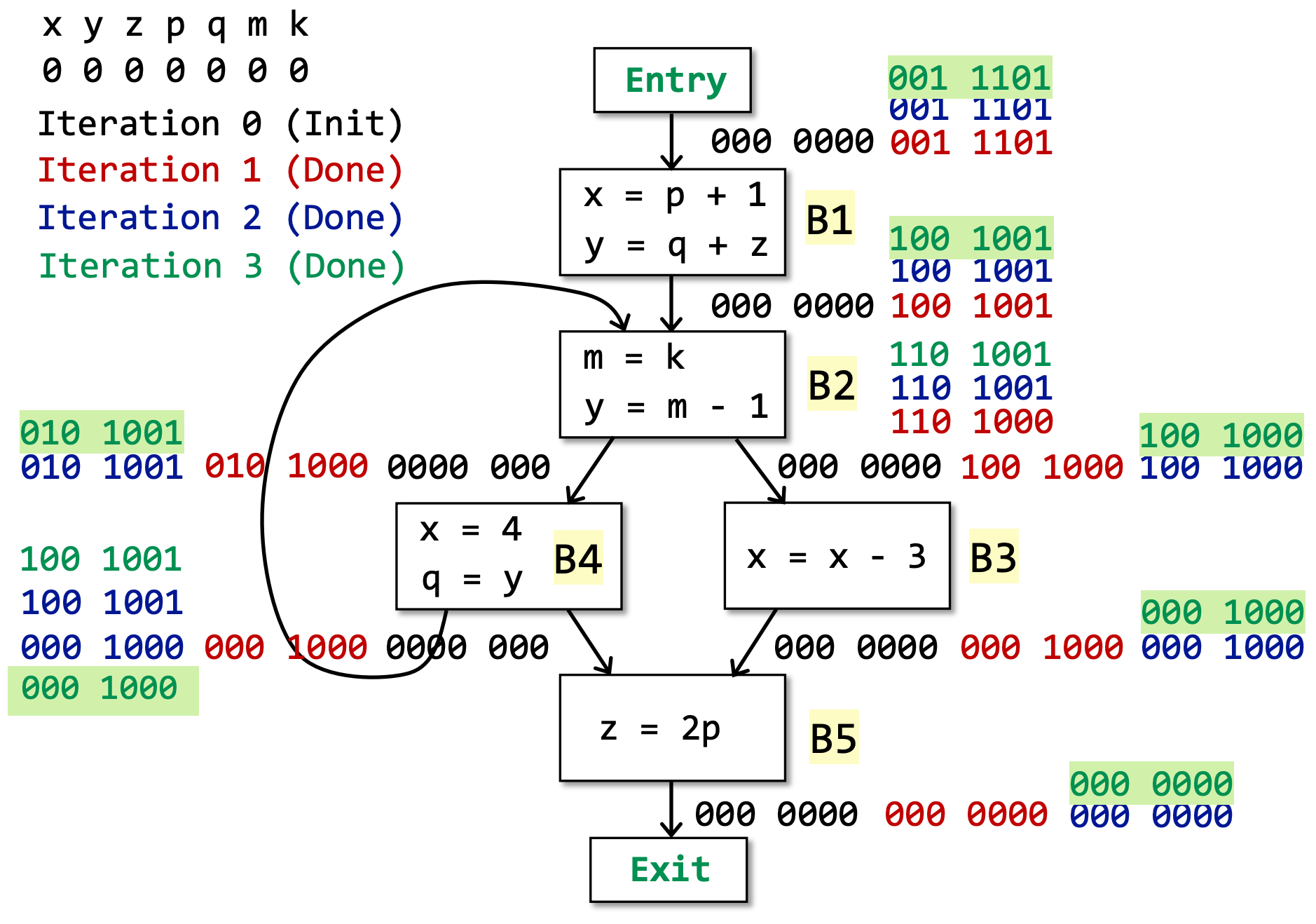
Transfer Function：IN[B] = use_B U (OUT[B] - def_B);
use_B是 BB 中使用过的变量。如果你在 BB 中使用了变量，那说明该变量是从 IN[B]传入的。
OUT[B]顾名思义，当前 BB 的 OUT。该算法是 backwards direction。
def_B是指，如果当前 BB 中重新定义了变量 v，那么说明该 v 不是从 IN[B]中传入的，也就是 dead 的，应该将其置为 0
Control Flow：OUT[B] = U_{S a successor of B} IN[S];
该算法采用 may analysis，因此如果遇到分支汇合的情况，取所有分支的并集∪。
该算法是 backwards direction。

Algorithm

INPUT: CFG (def_B and use_B computed for each basic block B)

OUTPUT: IN[B] and OUT[B] for each basic block B

算法如下：

IN[exit] = ∅;
for (each basic block B\exit){
  IN[B] = ∅;
}
while (changes to any IN occur){            // 该算法是backwards direction，因此当 IN 发生改变时，继续循环，而不是OUT。
  for (each basic block B\exit) {
    OUT[B] = U S a successor of B IN[S];    // 即 Control Flow
    IN[B] = useB U (OUT[B] - defB);         // 即 Transfer Function
    }
}

Live-Variables-Analysis-Example

Available Expressions Analysis¶

Definitions

程序点 p 处的表达式 x op y 是 available(可替换) 需满足 2 个条件：

从 entry 到 p 点的 所有路径 必须经过 x op y
最后一次使用 x op y 之后，没有重定义操作数 x、y。如果重定义了 x 或 y，如x = a op2 b，则原来的表达式 x op y 中的 x 或 y 就会被替代

这个定义说明，在 p 处如果表达式 available，就可以将其替换为最后一次运算的结果，或者可以检测全局通用表达式。

Usage

available expressions 的分析结果可以用于探测 global common subexpressions

如果这个表达式自始至终是 available 的，就可以将其替换为 最后一次运算的结果，或者可以将其提取为全局通用表达式。

Abstraction

Data Flow Values/Facts：

All the expressions in a program
Can be represented by bit vectors
e.g., E1, E2, E3, E4, …, VE (8 definitions)
使用比特表示：00000000，1 表示该表达式 available

Safe-approximation

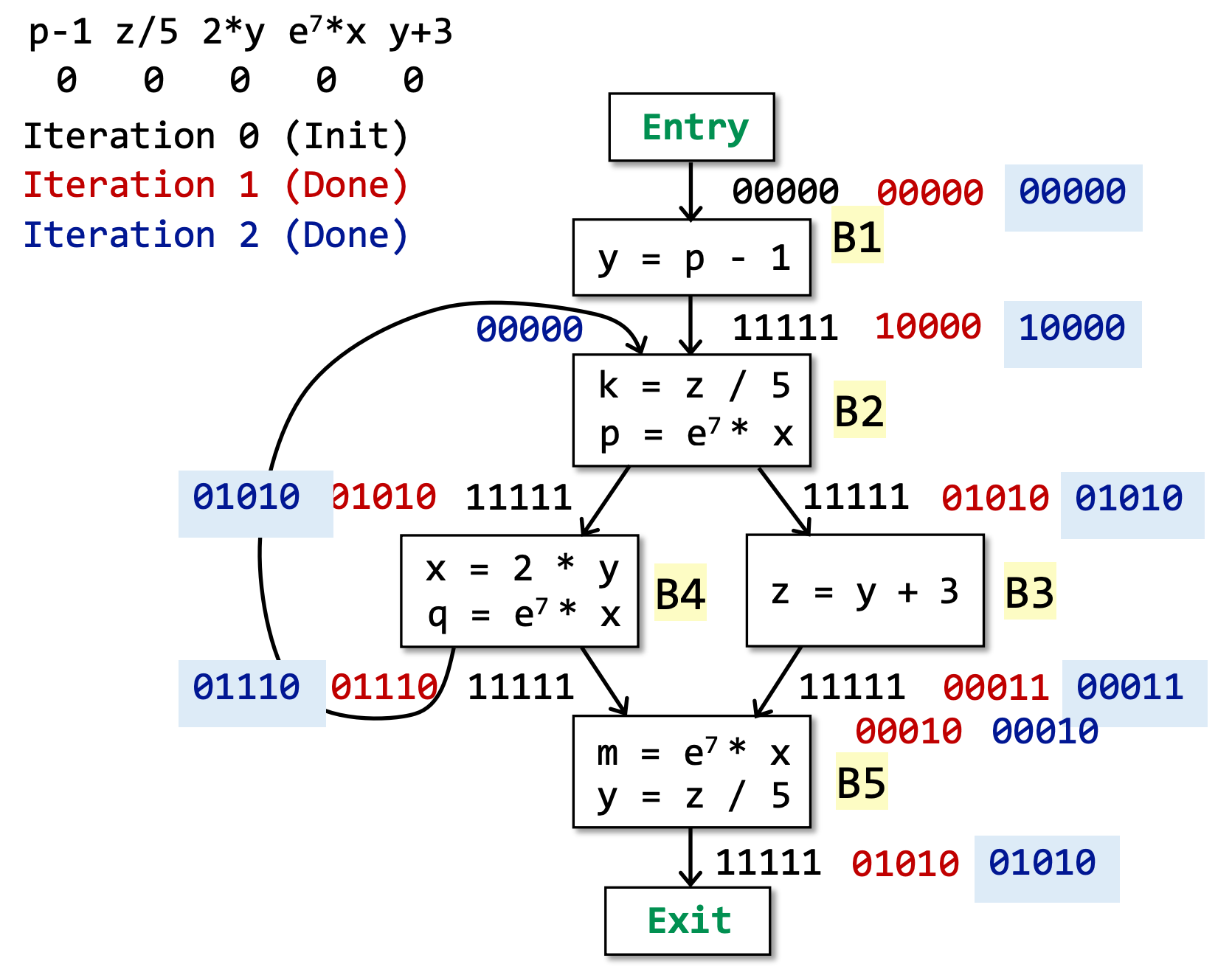
Transfer Function：OUT[B] = gen_B U (IN[B] - kill_B)
gen_B 表示区块中所有的表达式 x op y
OUT[B]顾名思义，当前 BB 的 OUT。该算法是 forwards direction。
kill_B是指，如果当前 BB 中存在对表达式中变量的重定义，例如：x = 1，此时需要将用到 x 的表达式都 kill 掉。
Control Flow：IN[B] = ∩ _{P a predecessor of B} OUT[P]
该算法采用 must analysis，因此如果遇到分支汇合的情况，取所有分支的交集。
该算法是 forwards direction。

Algorithm

INPUT: CFG (kill_B and gen_B computed for each basic block B)

OUTPUT: IN[B] and OUT[B] for each basic block B

算法如下：

OUT[entry] = ∅;
for (each basic block B\entry){
  OUT[B] = ∪;
  // 初始化为11111111（示例取8位）而不是00000000，其原因有很多，比如，由于是must analysis，因此取交集，若初始化为00000000，则0与任何值的交集都是0，就失去了意义！
}
while (changes to any OUT occur){            // 当 OUT 发生改变时，继续循环
  for (each basic block B\entry) {
    IN[B] = P a predecessor of B OUT[P];    // 即 Control Flow，所有上流分支的交集作为该BB的输入
    OUT[B] = genB U (IN[B] - killB);         // 即 Transfer Function
    }
}

Available-Expressions-Analysis-Example

summary¶

summary

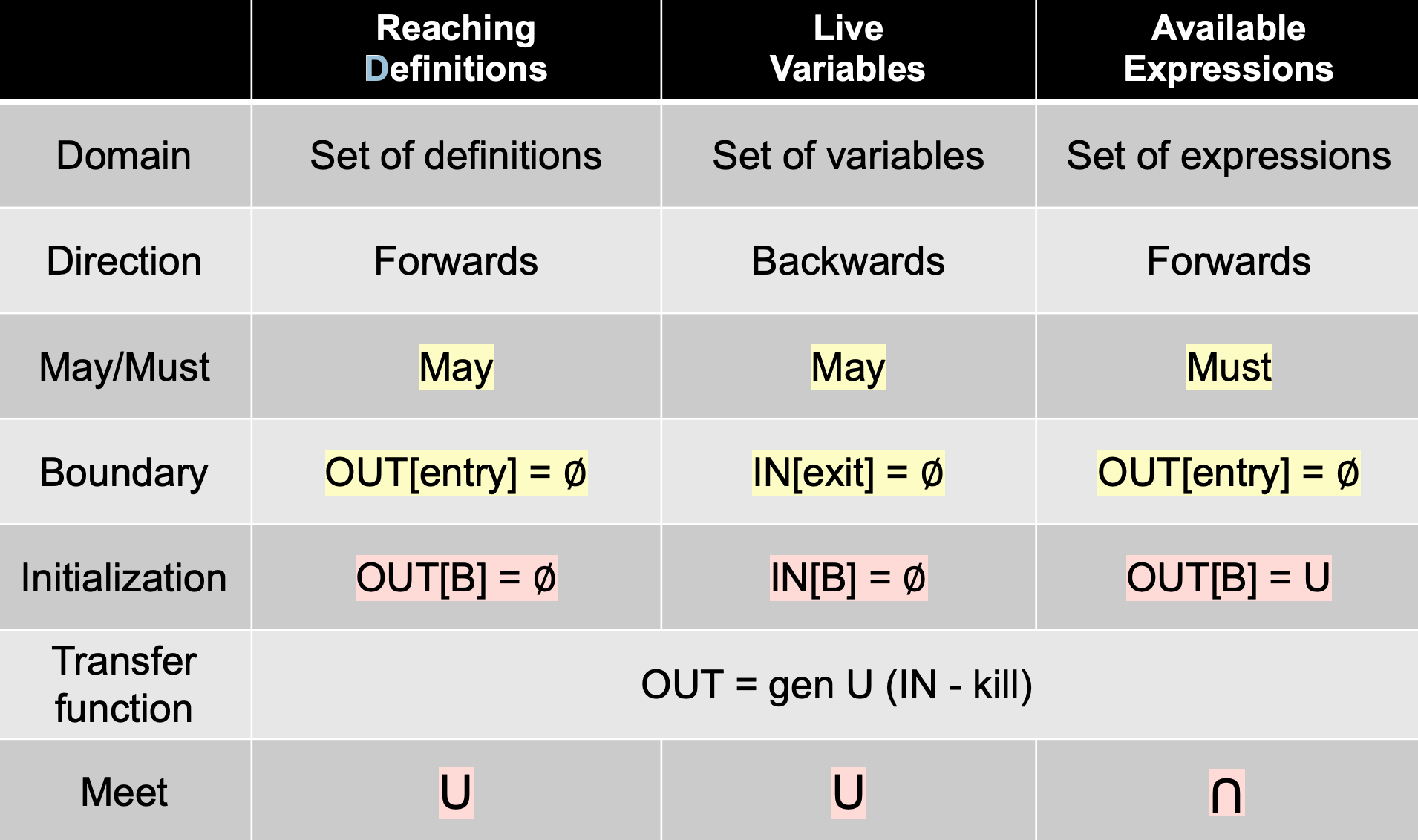
数据流分析理论基础¶

Iterative Algorithm, Another View¶

上节中，给出了三种静态分析应用的迭代算法逻辑，下面介绍上述迭代算法的另一种视角。

给定一个有 k 个节点 CFG，每个节点可以是 BB 或者 statement。此时迭代算法的工作是，在每次迭代的为每个节点时候更新 OUT[n]。
假设，数据流分析的 Domain of values 是 V，那么可以定义一个 k-tuple：(OUT[n₁], OUT[n₂], ..., OUT[n_k])，用于保存每次迭代后的分析结果。

$$ (OUT[n_1], OUT[n_2], ..., OUT[n_k])∈(V_1×V_2...×V_k)=V^k $$

(V₁ × V₂ ... × V_k) 是笛卡尔积。

每次迭代可以看做是通过 transfer functions 和 control-flow，将 old V^k更新为 new V^k，将其抽象为一个方法 F:V^k→V^k

iter-example

如图所示，经过 i+1 次迭代之后，会得到：X_i=X_i+1，此时到达不动点（Fixed Point），定义为：当 X=F(X)时，称 X 为不动点。

迭代算法提供了数据流分析的解决方法，但存在一些未能回答的问题：

算法是否确保一定能停止/达到不动点？会不会总是有一个解答？
如果能到达不动点，那么是不是只有一个不动点？如果有多个不动点，我们的结果是最优的吗？
什么时候我们会能得到不动点？

为了回答上述问题，需要一定的数学基础。

Partial Order¶

设 P 是集合，P 上的二元关系（记作 ≤）满足以下三个条件，则称“≤”是 P 上的偏序关系：

（1）自反性 Reflexivity：a≤a，∀a∈P；

（2）反对称性 Antisymmetry：∀a，b∈P，若 a≤b 且 b≤a，则 a=b；

（3）传递性 Transitivity：∀a，b，c∈P，若 a≤b 且 b≤c，则 a≤c；

注：此处的 ≤ 并非是小于等于，而是偏序关系。

具有偏序关系的集合 P 为偏序集（或称半序集，poset），记为（P，≤）。

例子，问 (S, ≤) 是否是偏序集合：

若 S 是整数集合，≤ 代表小于等于，则 S 是偏序集合
若 S 是整数集合，≤ 代表小于，则 S 不是偏序集合（不满足自反性，因为不满足 1 < 1）
若 S 是英文单词的集合，≤ 代表子集关系，即 sing ≤ singing，表示前者是后者的子集，此时 S 也是满足上述三个特性的，因此 S 也为偏序集合

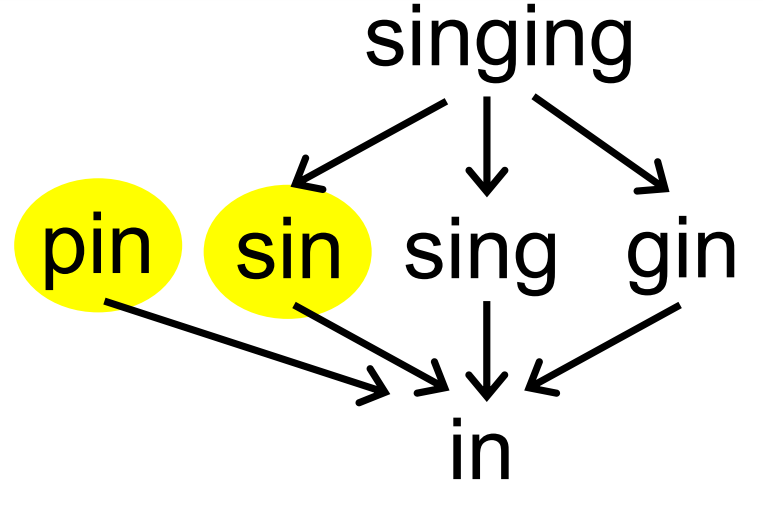
poset-example

若 S 是集合 {a,b,c} 的

如图所示，偏序集合中的任意两个元素可能没有任何关系，例如 pin 和 sin。

Upper and Lower Bounds¶

对于偏序集 P 中的某子集 S 来说：

若存在元素 u ∈ P，对于任意 x ∈ S，都满足 x ≤ u，此时称 u 是 S 的上界（Upper bound）。
类似的，若存在元素 l ∈ P，对于任意 x ∈ S，都满足 l ≤ x，此时称 l 是 S 的下界（Lower bound）。

然后我们衍生出最小上界和最大下界的概念：

最小上界（lub or join），记作 ⊔S，对于 S 的任意上界 u，满足 ⊔S ≤ u。
类似的，最大下届（glb or meet），记作 ⊓S，对于 S 的任意下界 l，满足 l ≤ ⊓S

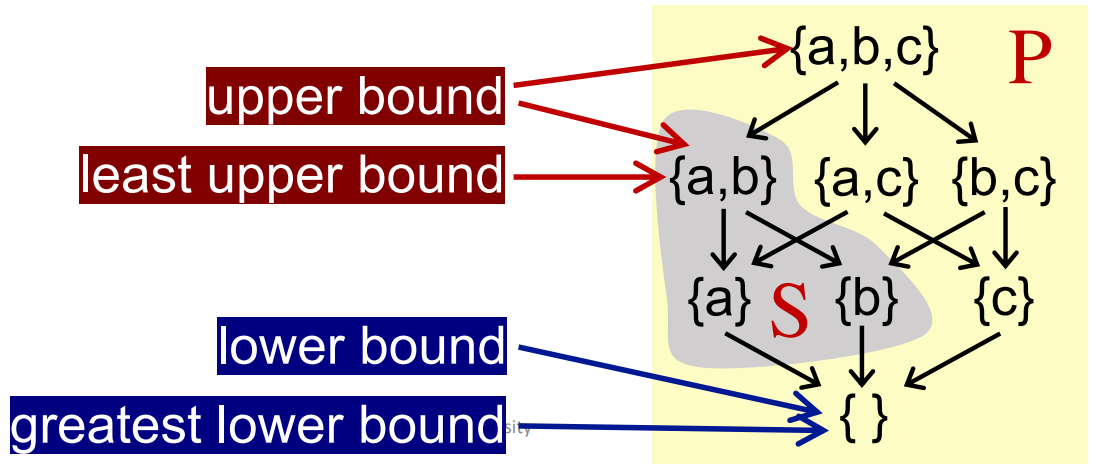
bound-example

通常，如果 S 中仅包含两个元素 a 和 b（S={a, b}，那么：

⊔S can be written a ⊔ b (the join of a and b)
⊓S can be written a ⊓ b (the meet of a and b)

并不是每个偏序集都有 lub 和 glb，但是如果有，那么该 lub, glb 将是唯一的。

no-glb-example

// 证明唯一
assume g1 and g2 are both glbs of poset P
according to the definition of glb
g1 ⊑ (g2 = ⊓P) and g2 ⊑ (g1 = ⊓P)
by the antisymmetry of partial order ⊑
g1 = g2

Lattice, Semilattice, Complete and Product Lattice¶

（1）Lattice 格

Given a poset (P, ⊑), ∀a, b ∈ P, if a ⊔ b and a ⊓ b exist, then (P, ⊑) is called a lattice

通俗的说，如果一个偏序集中的 任意两个元素，都存在最小上界和最大下界，那么这个偏序集称为 Lattice。

（2）Semilattice 半格

Given a poset (P, ⊑), ∀a, b ∈ P,

if only a ⊔ b exists, then (P, ⊑) is called a join semilattice
if only a ⊓ b exists, then (P, ⊑) is called a meet semilattice

通俗的说，就是只存在一个上界或下界。

（3）Complete Lattice

Given a lattice (P, ⊑), for arbitrary subset S of P, if ⊔S and ⊓S exist, then (P, ⊑) is called a complete lattice

通俗的说，如果一个偏序集的所有子集，都存在最小上界和最大下届，那么这个偏序集称为 Complete Lattice。

例如，当 P 为整数集合，⊑ 为小于等于关系时。(P, ⊑) 不是一个完备格。因为对于所有正整数构成的子集，它不存在上界，也就不存在 ⊔S。

Every complete lattice (P, ⊑) has

a greatest element = ⊔P called top
a least element ⊥ = ⊓P called bottom

结合 Lattice 的定义，可以得知：Every finite lattice (P is finite) is a complete lattice

有穷的 lattice 一定是 Complete Lattice
但 Complete Lattice 不一定是有穷的 lattice。（e.g. 0 和 1 之前所有的实数，无穷多，但有 top 和 bottom，所以是 Complete Lattice。

（4）Product Lattice

Given lattices L₁ = (P₁, ⊑1), L₂ = (P₂, ⊑2), …, L_n = (P_n, ⊑n), if for all i, (P_i , ⊑_i ) has:

⊔_i (least upper bound)
and ⊓_i (greatest lower bound),

then we can have a product lattice L_n = (P, ⊑) that is defined by:

P = P₁ × … × P_n

笛卡尔积

(x₁, …, x_n) ⊑ (y₁, …, y_n) ⟺ (x₁ ⊑ y₁) ∧ … ∧ (x_n ⊑ y_n)
(x₁, …, x_n) ⊔ (y₁, …, y_n) = (x₁ ⊔₁ y₁, …, x_n ⊔_n y_n)
(x₁, …, x_n) ⊓ (y₁, …, y_n) = (x₁ ⊓₁ y₁, …, x_n ⊓_n y_n)

其性质如下：

一个 product lattice 也是一个 lattice
if a product lattice L is a product of complete lattices, then L is also complete

Data Flow Analysis Framework via Lattice¶

data flow analysis framework (D, L, F) consists of:

D: a direction of data flow: forwards or backwards
L: a lattice including domain of the values V and a meet ⊓ or join ⊔ operator
F: a family of transfer functions from V to V

数据流分析可以看作是迭代地使用 transfer functions 和对 lattice 的值进行 meet/join 操作。

Monotonicity and Fixed Point Theorem¶

回看我们在上面提出的问题：迭代算法在什么条件下可以停机？我们在这里引入不动点定理

（1）Monotonicity

A function f: L → L (L is a lattice) is monotonic if ∀x, y ∈ L, x ⊑ y ⟹ f(x) ⊑ f(y)

单调性，即 x 小于 y，则 f(x) 小于 f(y)

（2）Fixed Point Theorem

给定一个 complete lattice (L, ⊑)，如果：

f: L → L 是单调的（Monotonicity）
L 是有穷的（finite）

那么

迭代 f(⊥), f(f(⊥)), …, f^k(⊥) 可以得到最小不动点（least fixed point）。
迭代 f(T), f(f(T)), …, f^k(T) 以得到最大不动点（greatest fixed point）。

可以证明（参见PDF，视频 1:25:00）：

不动点是存在的
不动点是最小不动点（最优）

fixed-point-theorem

fixed-point-theorem2

Relate Iterative Algorithm to fixed Point Theorem¶

以上我们只是定性的描述了是否能得到最优不动点，但是迭代算法怎样才能算是符合了不动点定理的要求呢？

证明略。

最后我们再列出这三个问题与其回答：

算法是否确保一定能停止/达到不动点？能！会不会总是有一个解答？可以！
如果能到达不动点，那么是不是只有一个不动点？可以有很多。 如果有多个不动点，我们的结果是最优的吗？是的！
什么时候我们会能得到不动点？最坏情况下，是 lattice 的高度与 CFG 的节点数的乘积。

May/Must Analysis, A Lattice View¶

无论 may 还是 must 分析，都是从一个方向到另一个方向去走。

（1）may analysis

对于 Data Flow Analysis Applications 中的 Reaching Definitions Analysis，该算法采用 may 分析，该算法的 Lattice 表示如图右所示。

下界代表没有任何可到达的定值，上界代表所有定值都可到达。

下界代表 unsafe 的情形，即我们认为无到达定值，可对相关变量的存储空间进行替换。上界代表 safe but useless 的情绪，即认为定值必然到达，但是这对我们寻找一个可替换掉的存储空间毫无意义。

而因为我们采用了 join 函数，那么我们必然会从 lattice 的最小下界往上走。而越往上走，我们就会失去更多的精确值。那么，在所有不动点中我们寻找最小不动点，那么就能得到精确值最大的结果。

may-analysis-example

如图，假设上图代表是否可达，例如 {a,b,c} 代表定义 a,b,c 均可达，如果以比特数组表示，即为 111；{a,c} 则代表 a,c 可达，比特数组为 101.

如果 truth 为 {a,c}，那么，{a,b,c} 虽然有误报，但还是 safe 的，只是精度降低，而其余的结果均为 unsafe，因为存在漏报。

根据上述的不动点定理，给定一个 complete lattice (L, ⊑)，如果：

f: L → L 是单调的（Monotonicity）
L 是有穷的（finite）

那么 may analysis 最终求出的不动点一定是最小不动点。

正常来说，在分析的时候，必须要走到 safe 里分析才有用，当然越准越有用，也就是不动点越小越好。

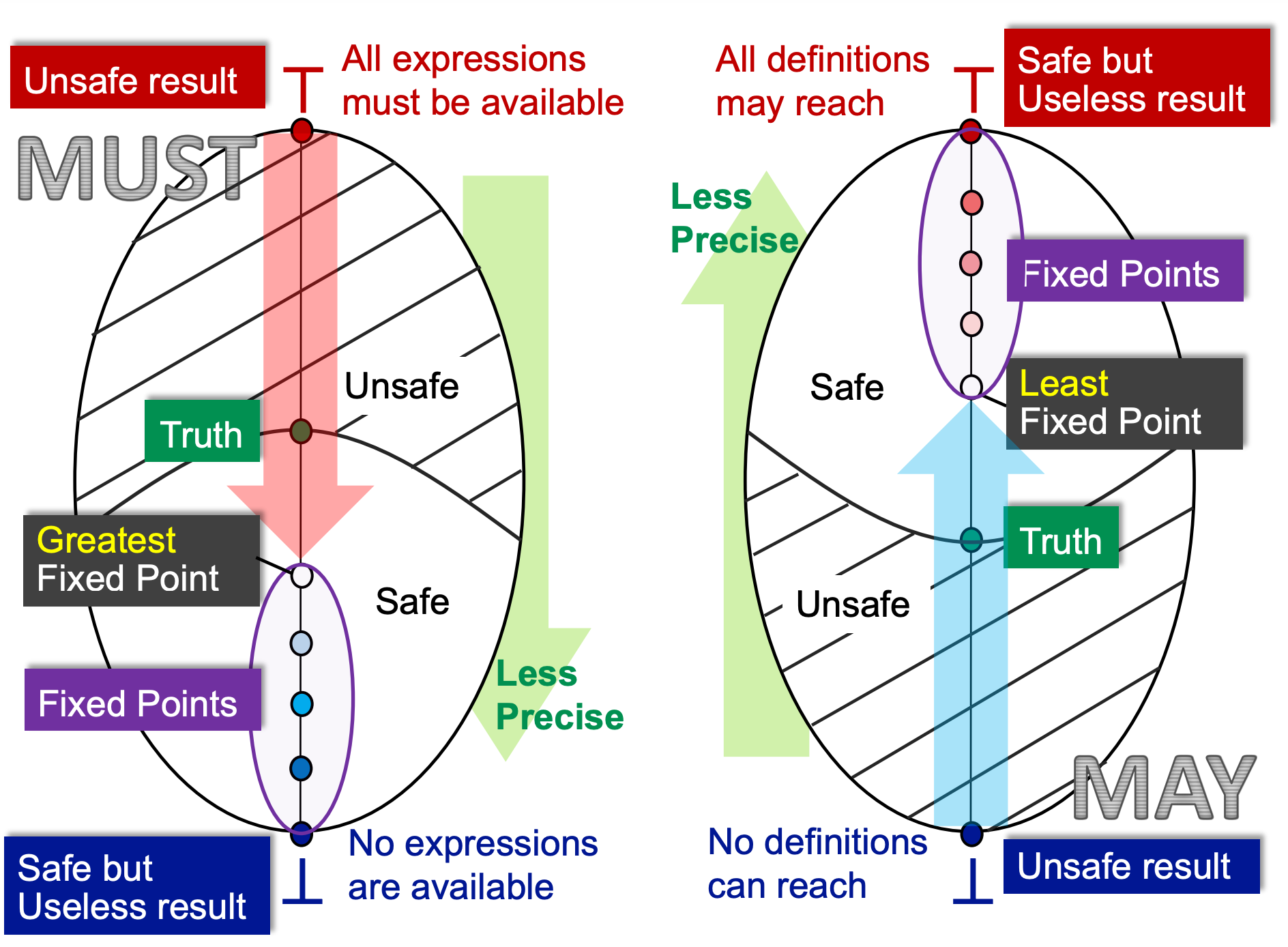
must-may-analysis

（2）must analysis

对于 Data Flow Analysis Applications 中的 Available Expressions Analysis，该算法采用 must 分析，该算法的 Lattice 表示如图做所示。

如果一个表达式是 available 的，说明该表达式可以替换为最后一次运算的结果，或可以检测全局通用表达式，我们用“可优化的”来统称。

此时，如图的上界，即 11...11 表示所有表达式都是可优化的，这显然是不安全的，因为可能把不能优化的表达式优化了，而下界 00...00 则表示所有表达式都不能优化，这肯定是安全的，因为他啥也没改，但也是无用的。

因此我们要在 safe 的区域里寻找一个最大不动点，此时可以得到最精准的结果，而上文介绍的不动点定理，must analysis 求出的一定是最大不动点。

Distributivity and MOP¶

我们引入 Meet-Over-All-Paths Solution，即 MOP。在这个 solution 中，我们不是根据节点与其前驱/后继节点的关系来迭代计算数据流，而是 直接查找所有路径，根据所有路径的计算结果再取上/下界。这个结果是最理想的结果。

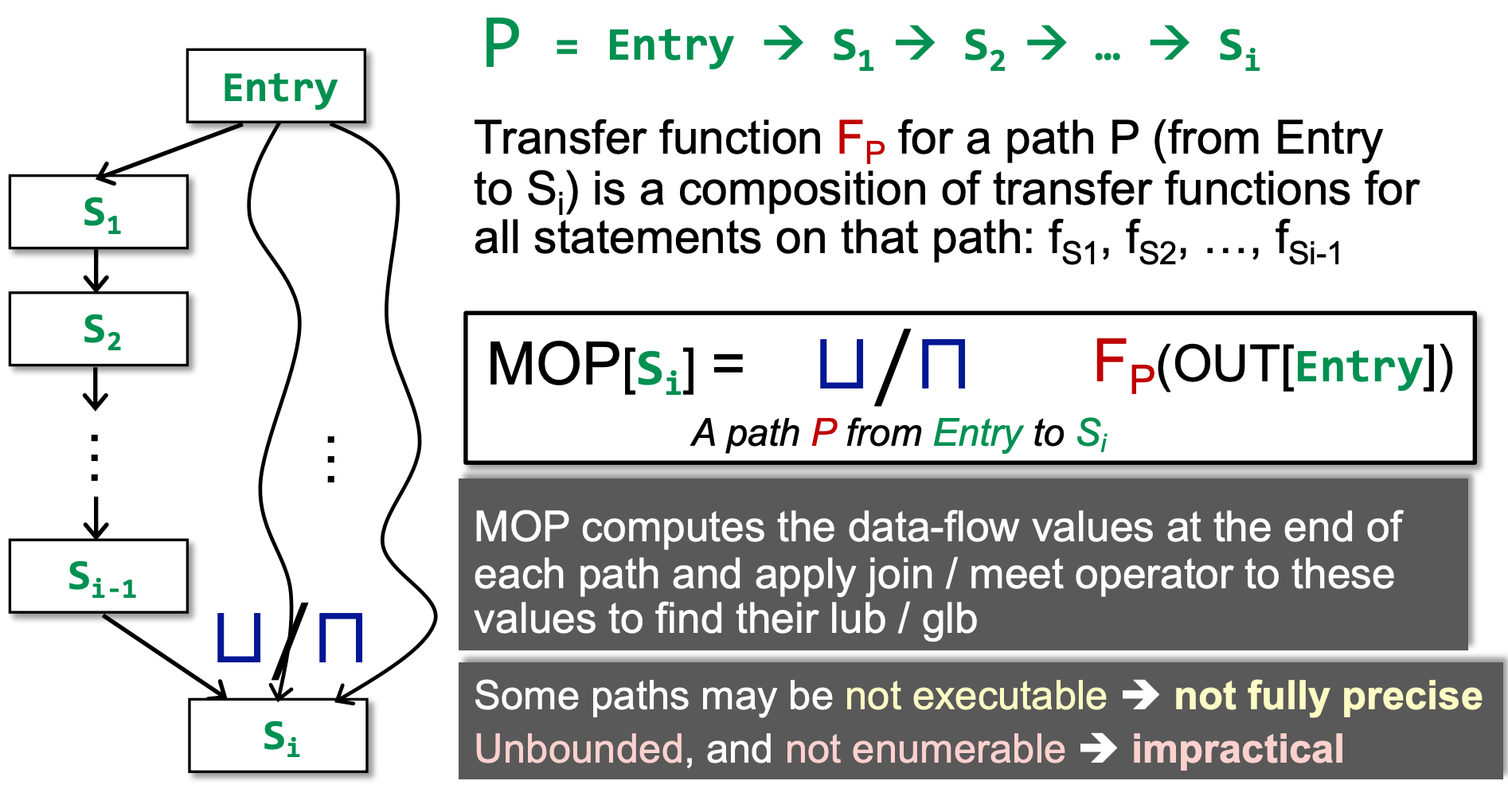
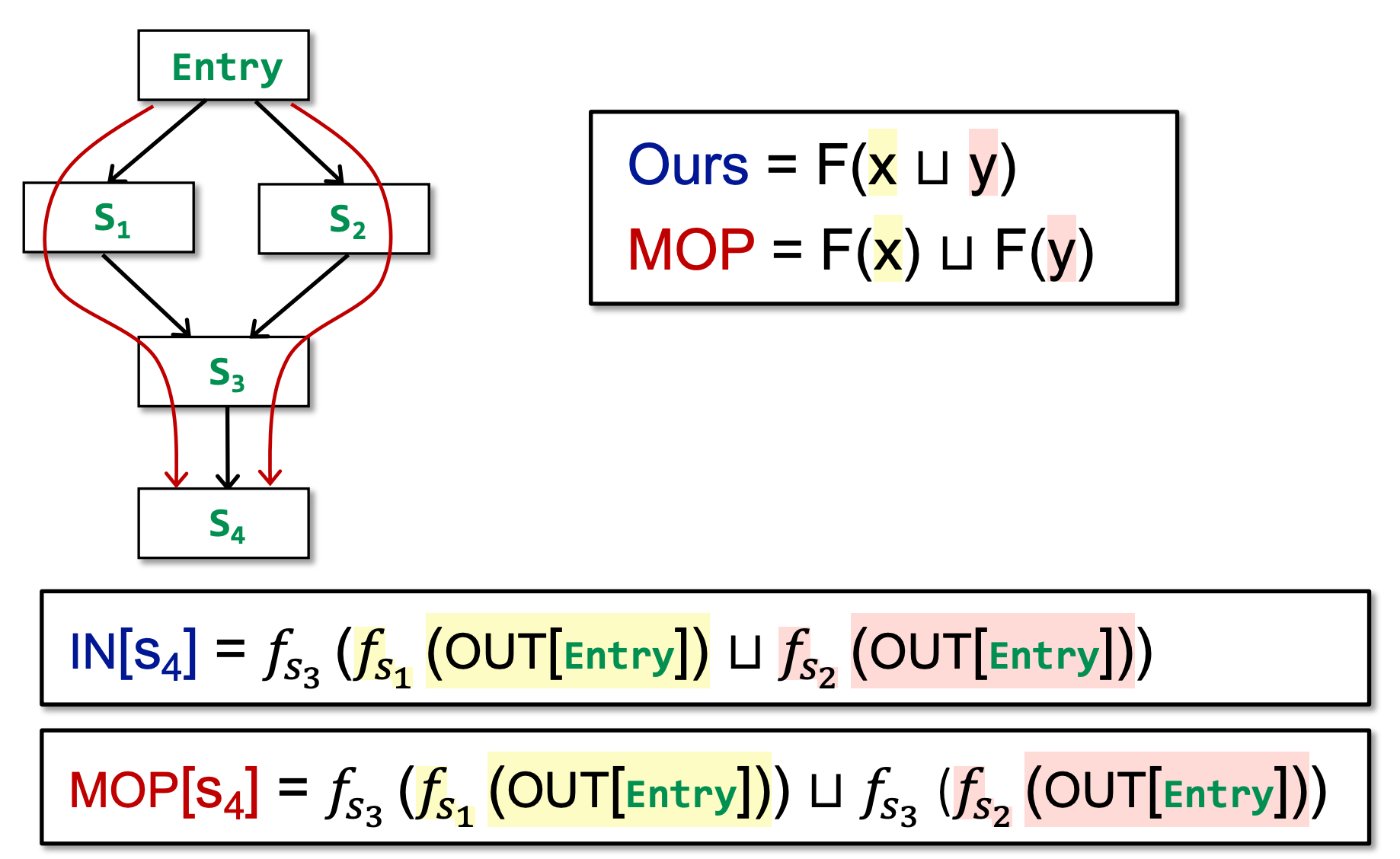
可以看到，迭代算法是 s3 对前驱取 join 后进行进行 f3 的转移，而 MOP 算法是对到达 s3 之后，s4 之前的路径结果取 join。

那么，我们的迭代算法和 MOP 算法哪个更加精确呢？

iter_vs_mop

当 F 是 distributive 的时候，二者精度相同，否则，MOP 精度大于我们的迭代算法。

Bit-vector or Gen/Kill problems (set unio n /intersection for join/meet) are distributive！

Constant Propagation¶

TODO 这里是作业，待补充

当然有些问题下 F 不是 distributive 的，如常量传播（Constant Propagation）。在常量传播分析中，其最大上界是 undefine，因为我们不知道一个变量到底被定义为了什么值。最小下界是 NAC（Not A Constant），而中间就是各种常量。这是因为分析一个变量指向的值是否为常量，那么要么它是同一个值，要么它不是常量。

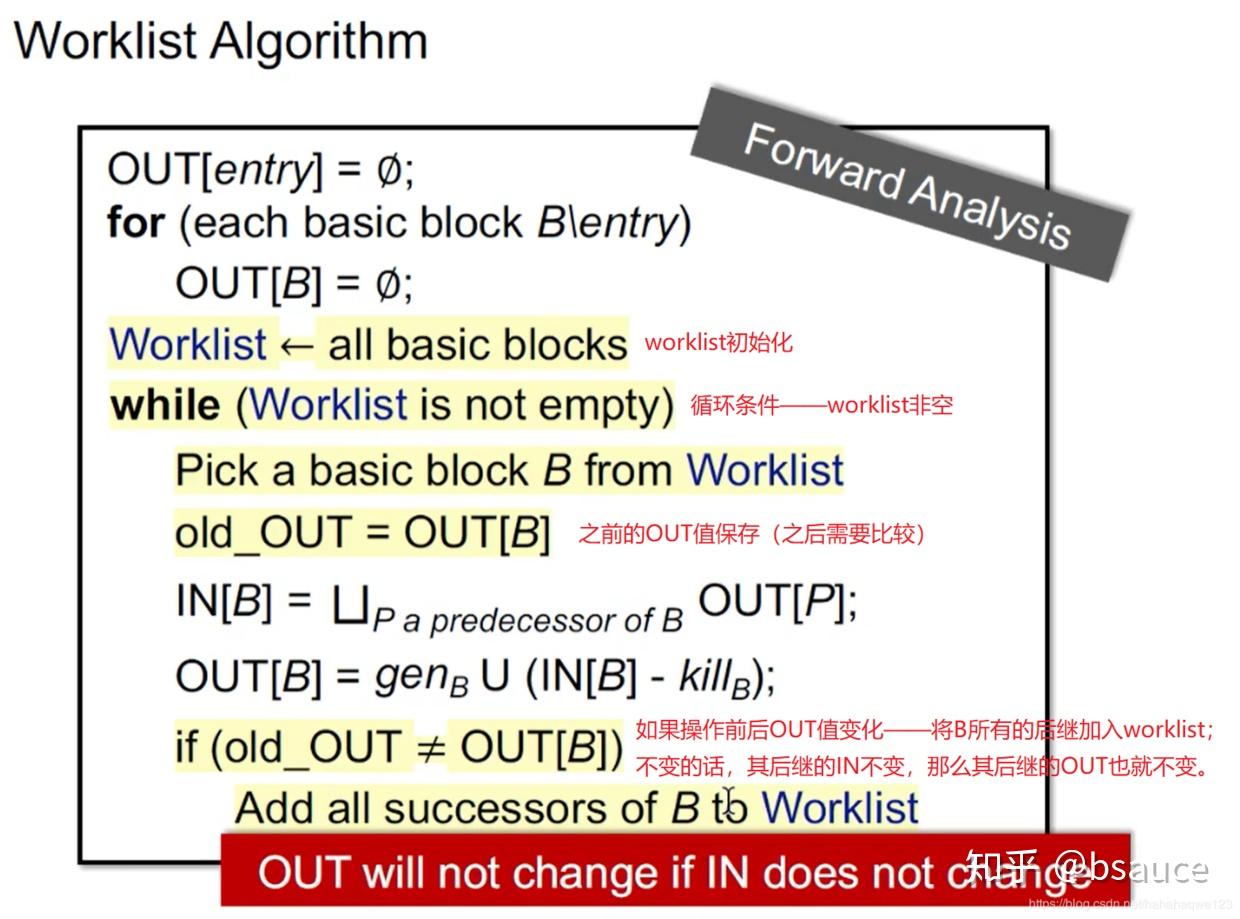
Worklist Algorithm¶

worklist 是迭代算法的优化，所以业界一般都不会使用迭代算法，而是使用优化的 worklist 算法。

worklist

过程间分析¶

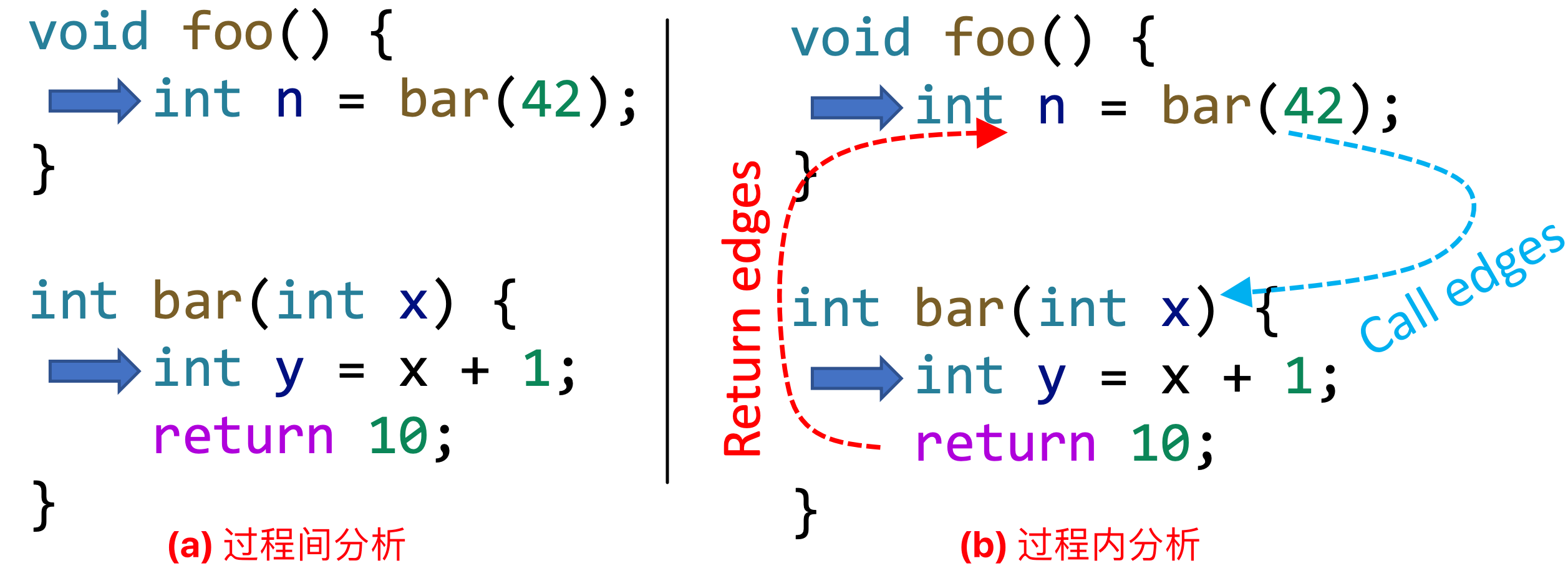
为什么要使用过程间分析（Interprocedural Analysis）？

在过程内分析时，仅对单个方法进行静态分析，若出现了对别的方法的调用，为了确保分析的正确性，只能认为该调用可能会做任何事情，从而使得分析结果不够准确。

对下述程序进行常量传播分析时，图(a)时过程内分析，当遇到方法调用时，对该方法保守分析，因此最终分析结果如下：

x = NAC, y = NAC
n = NAC

为了更好的精度，需要进行过程间分析，由于传入 bar() 方法的是常量，其返回也是常量，以此类推，可得分析结果：

x = 42, y = 43
n = 10

inter-vs-intra-analysis

Call Graph¶

Call Graph 是程序中调用关系的表示方式，本质上 Call Graph 是调用边的集合。

调用边：从 call-site 指向目标方法（callees）

我们认为 call-site 就是调用方法的点，例如 a.foo() 就是一个 call-site。

Call Graph 有很多应用：过程间分析的基础，程序的优化、理解、debug、测试 ……

对于面向对象的语言（OOPLs），Call Graph 的构造方式有很多，本课程主要关注：

类层次分析（CHA，Class Hierarchy Analysis）：效率高
指针分析（k-CFA，Pointer Analysis）：精确度高

cg-construction

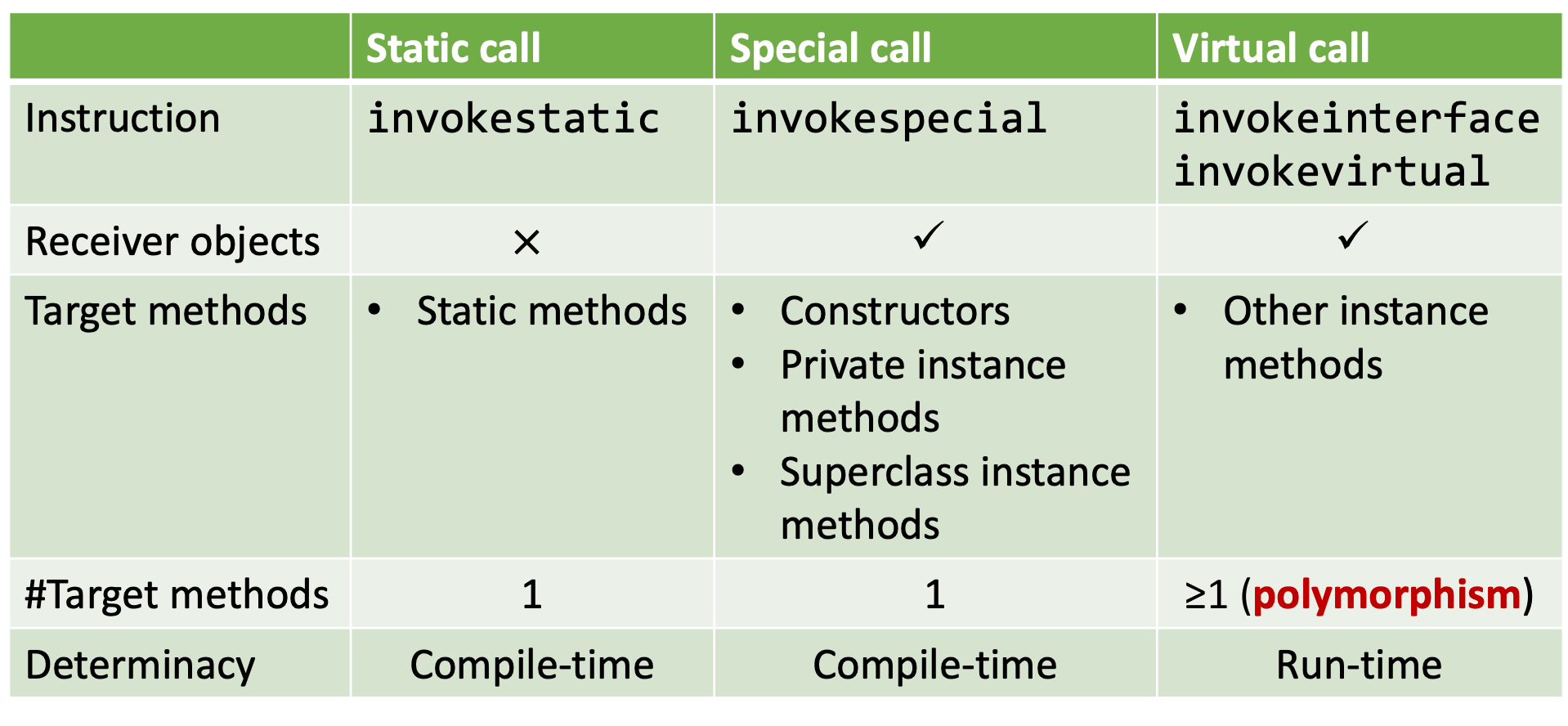
JAVA 中的方法调用共有五种，其中 invokedynamic 在此不做考虑：

Static Call、Special Call：调用的方法可在编译时确定
Virtual Call 的目标方法需要运行时动态确定的（多态）

因此，构造调用图的难点和关键在于如何处理 Virtual Call。

java-method-call

在 Virtual Call 时，是如何进行 Method Dispatch 的呢？

例如，对于一个 Virtual Call 为：o.f(...)，其在运行时基于两点来 resolve

c：receiver object 的类型，即变量 o 指向的对象的类型
m：call-site 的方法签名，在本课程中，方法签名被定义为：

method-signature

基于上述内容，定义方法 Dispatch(c,m) 来模拟运行时的方法分派。

method-dispatch

其流程可以概括为，优先在当前对象类中寻找方法，若没有找到，则在其父类中寻找，这就是 Java 中多态的执行逻辑，只是用形式化的语言表达出来而已。

class A {
  void foo() {…}
}
class B extends A {
}
class C extends B {
  void foo() {…}
  }
  void dispatch() {
    A x = new B()
    x.foo();       // 此处是 call-site，变量 x 执行的对象的类型是 B，其方法签名是 A.foo()
                                 // 为什么对象类型是 B？因为是 new 的 B 对象。
                                 // 为什么方法签名是 A.foo()? 因为接收类型是 A
                                 // Dispatch(B, A.foo()) = A.foo()
                                 // 为什么返回 A.foo()，因为在类型 B 中没有找到具有相同 name 和 descriptor 的方法
                                 // 于是递归调用 Dispatch 方法到其父类 A 中寻找具有相同 name 和 descriptor 的方法，而且刚好找到！
    A y = new C();
    y.foo();       // call-site, Dispatch(C, A.foo()) = C.foo()
                                 // 在类型 C 中直接找到了具有相同 name 和 descriptor 的方法
  }
}

① 类层次分析（CHA, Class Hierarchy Analysis)¶

IDE 中的类型跳转等功能就是通过 CHA 实现的，该算法快但并不精准，适用于快速分析并对准确性没有较高的要求的领域。

该算法需要所有整个程序的类继承结构信息，基于 call site 处的 receiver variable 的 declared type 进行分析：

A a = ...
a.foo(); //call site

上例中：receiver variable 是 a，其 declared type 是 A。

该算法假设变量 a 可能指向 A 或其所有的子类，这种假设也意味着误报的存在，这也是后续学习指针分析的原因。

CHA 通过定义方法 Resolve(cs) 来计算 call-site(cs) 可能调用的目标方法。

CHA-Resolve

该算法对方法调用的类型进行分类讨论：

静态方法调用：目标方法就是 call-site 调用的方法，因为 Java 中静态调用是直接用类名调
特殊调用：
私有函数、构造函数：直接可以找到
父类方法：需要递归查找

因此，为了形式统一，此处使用 Dispatch 表示。

虚拟调用：即普通的函数调用，不断地递归寻找子类中的方法签名，并将其加入到 target method 列表 T 中。

CHA-example

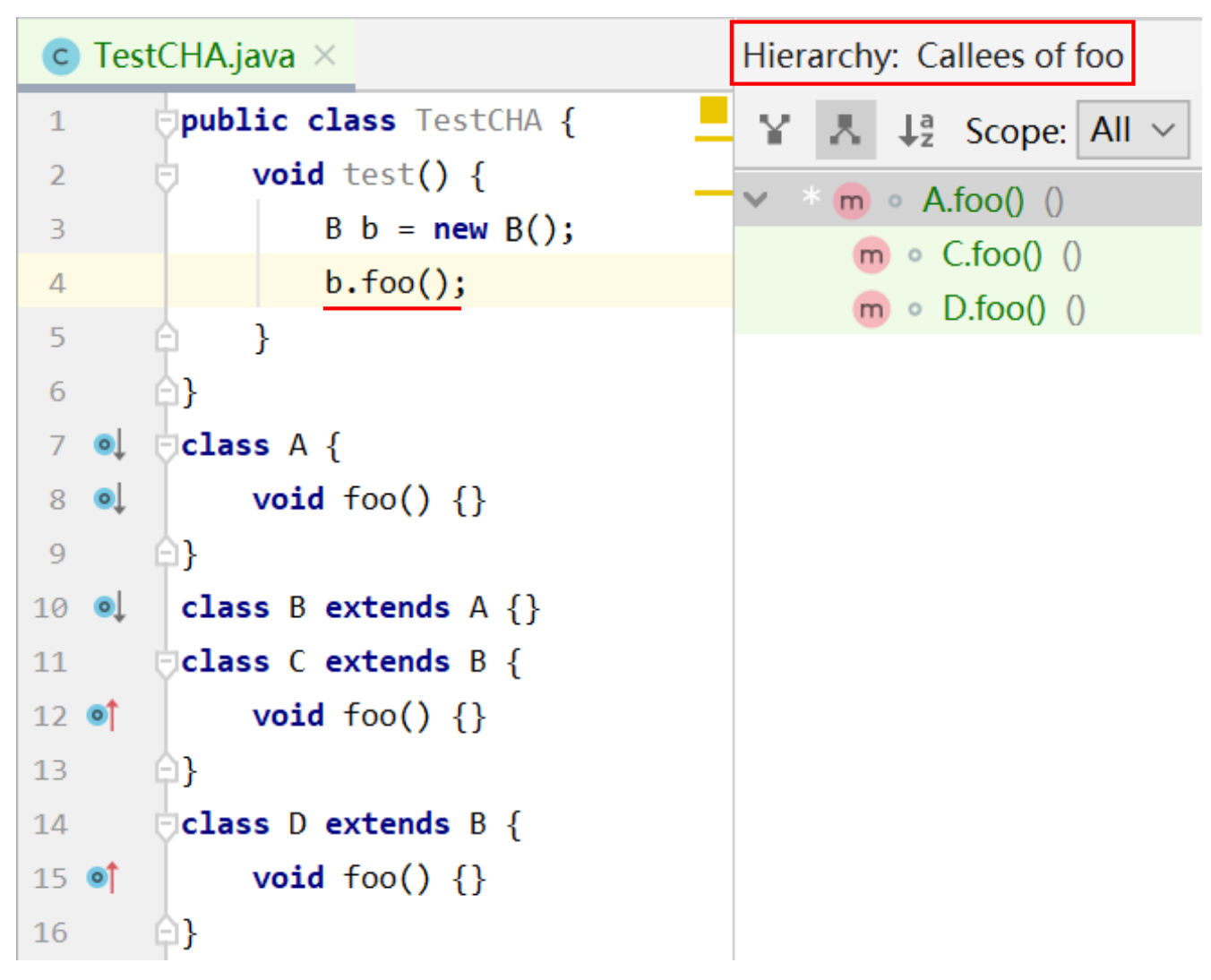
对于 call-site c.foo() 而言，由于其没有子类，因此只有一个可能的目标方法 {C.foo()}；

对于 call-site a.foo() ，寻找自身及所有子类中具有相同方法名和方法描述的方法，加入目标列表；

对于 call-site b.foo()，首先，在 Resolve 中，会对 b 的声明类型，也就是 B，及其所有子类，此处就是子类 C、D，均调用 Dispatch 方法：

首先调用 Dispatch(B,B.foo())。在 Dispatch 内部，则会向上查找，也就是先在当前类（B）中寻找具有相同 name 和 descriptor 的方法，由于 B 中没有，因此找其父类 A 中是否存在，在 A 中存在，则将找到的结果写入 T 中。

Dispatch(B,B.foo()) 方法中，似乎第二个 B 是没有用到的。

随后调用 Dispatch(C,B.foo())，在 C 中就找到了目标 C.foo()
同理，找到 D.foo()

注意理解 CHA 的误报，假设此处定义如下：

B b = new B();
b.foo();

最终 Resolve 的结果仍然是 {A.foo(), C.foo(), D.foo()}，而不是 {A.foo()}。虽然肉眼一眼就看出，不可能调用 C.foo() 或者 D.foo()，因为我们实例化的对象是 B，怎么可能调用它子类的方法呢？这就是 CHA 的缺陷！

Intellij IDEA 中就是采用 CHA 算法：

IDEA-CHA

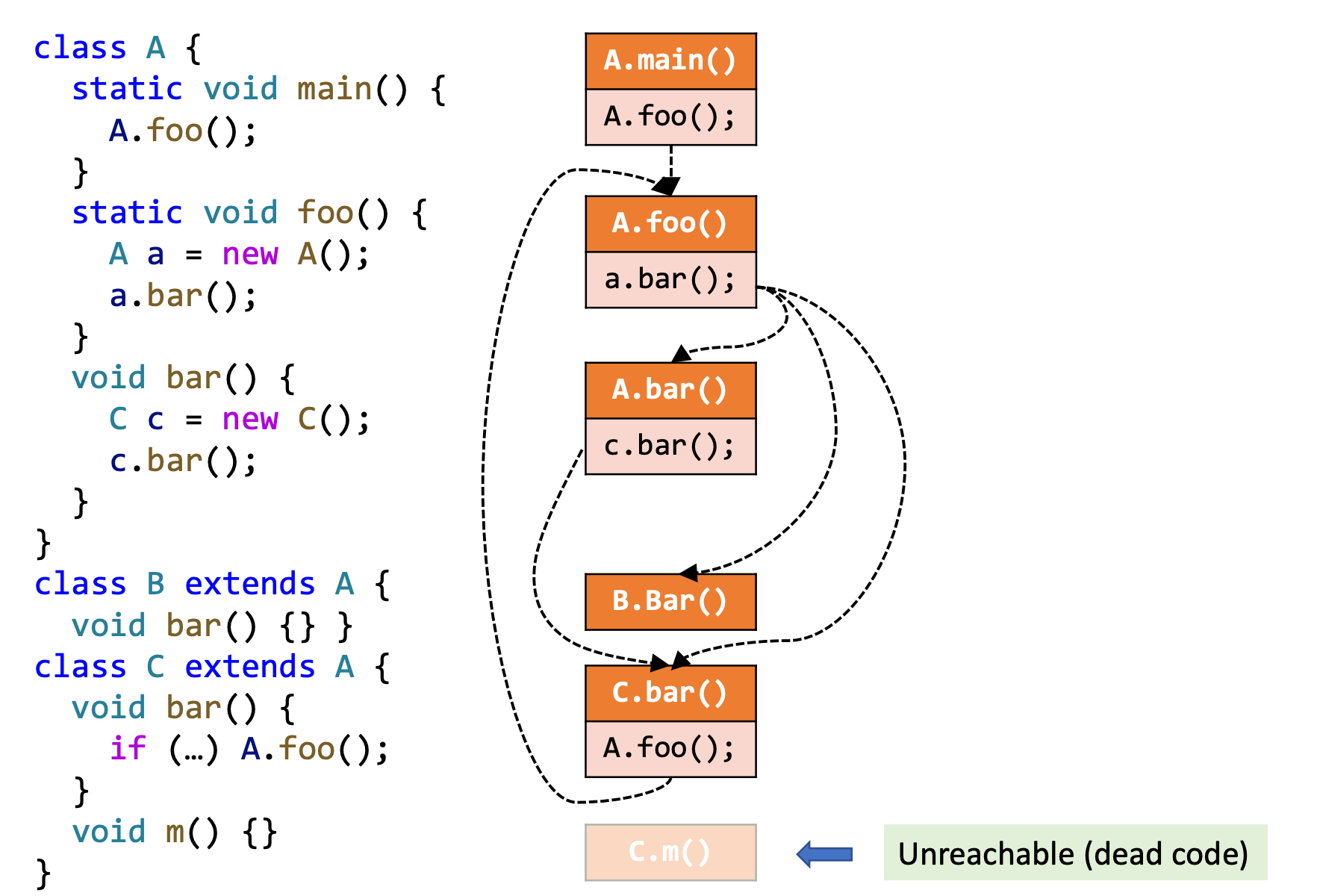
通过 CHA 构造 Call Graph¶

从入口方法（main）开始，对每一个可达的方法 m 中的每一个调用点 cs，解析目标方法（Resolve(cs)），重复该过程直到没有新的方法被发现。具体算法如下：

BuildCallGraph-By-CHA

WL：Work list, containing the methods to be processed
CG：Call graph, a set of call edges
RM： A set of reachable methods，避免重复分析同一个方法

CHA-CG-example

过程间控制流图（ICFG,Interprocedural Control-Flow Graph）¶

CFG 表征了单个方法内的结构，ICFG 则更全面的表达了整个程序的执行结构。

ICFG 图中除了 CFG 的信息外，还添加了额外的两类 edge：

Call edges：从 call-site 指向 callee 的 entry node
Return edges：从 callee 的 exit node 指向 call-site 的下一个语句

基于 ICFG 进行程序分析，其 Transfer Function 不仅需要正常的 Node Transfer 还要处理 Call Edge Transfer（用于传参）和 Return Edge Transfer（用于传递返回值）。

在本地方法的 CFG 中的 Node Transfer 需要把调用点的左值变量 kill 掉（Return Edge Transfer 会覆盖这些变量的值）。

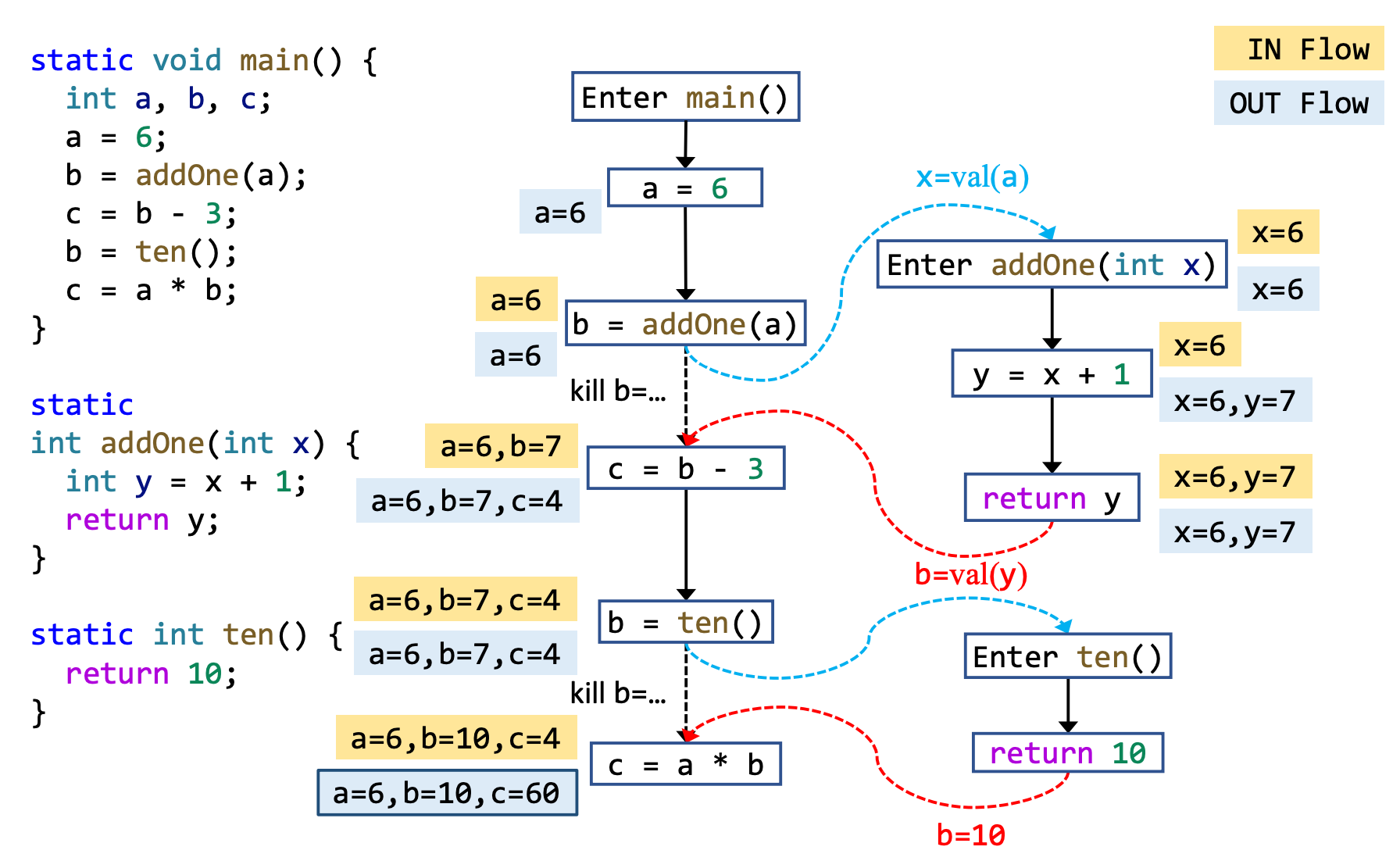
icfg-example

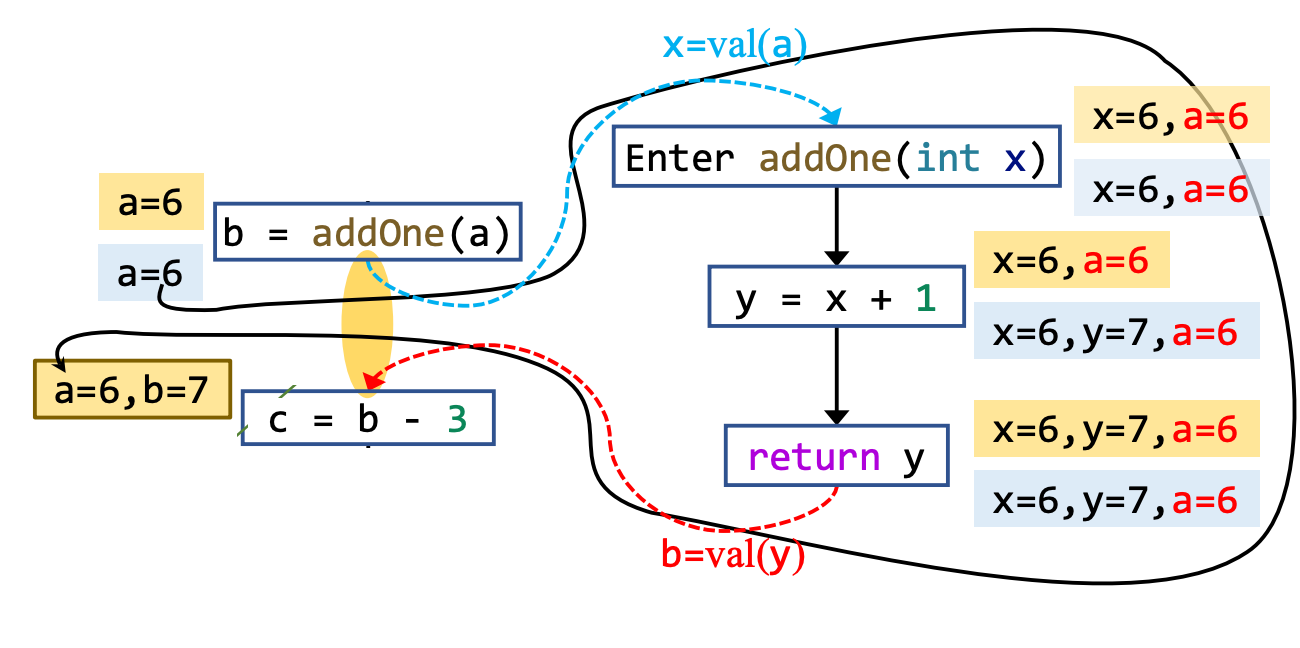
黄色背景的 edge 被称为：call-to-return edges，保留这条边可以有助于提升分析效率，如果没有该边的话，a 变量也需要随着 cg 一起分析。

call-to-return

② 指针分析¶

为什么需要指针分析？

在 CHA 中，曾举过一个例子：

B b = new B(); // B 具有子类 C、D
b.foo();

CHA 在解析 b.foo() 时会得到所有 B 类型及其子类的签名为 foo() 的方法，其中子类的 foo() 方法均为误报，因为 B 类型是父类，不可能调用子类的方法。

使用指针分析则可以找到唯一的一个目标方法，提高分析的准确性。

指针分析简介

静态分析的基石
常用于面向对象语言，计算一个指针（variable or field）能够指向哪些对象
指针分析可以看作一种 may analysis，计算结果是一个 over-approximation

概念辨析：指针分析 vs. 别名分析

指针分析回答的问题：Which objects a pointer can point to ?
别名分析回答的问题：Can two pointers point to the same object ?

别名分析的结果可由指针分析的结果推到而来。

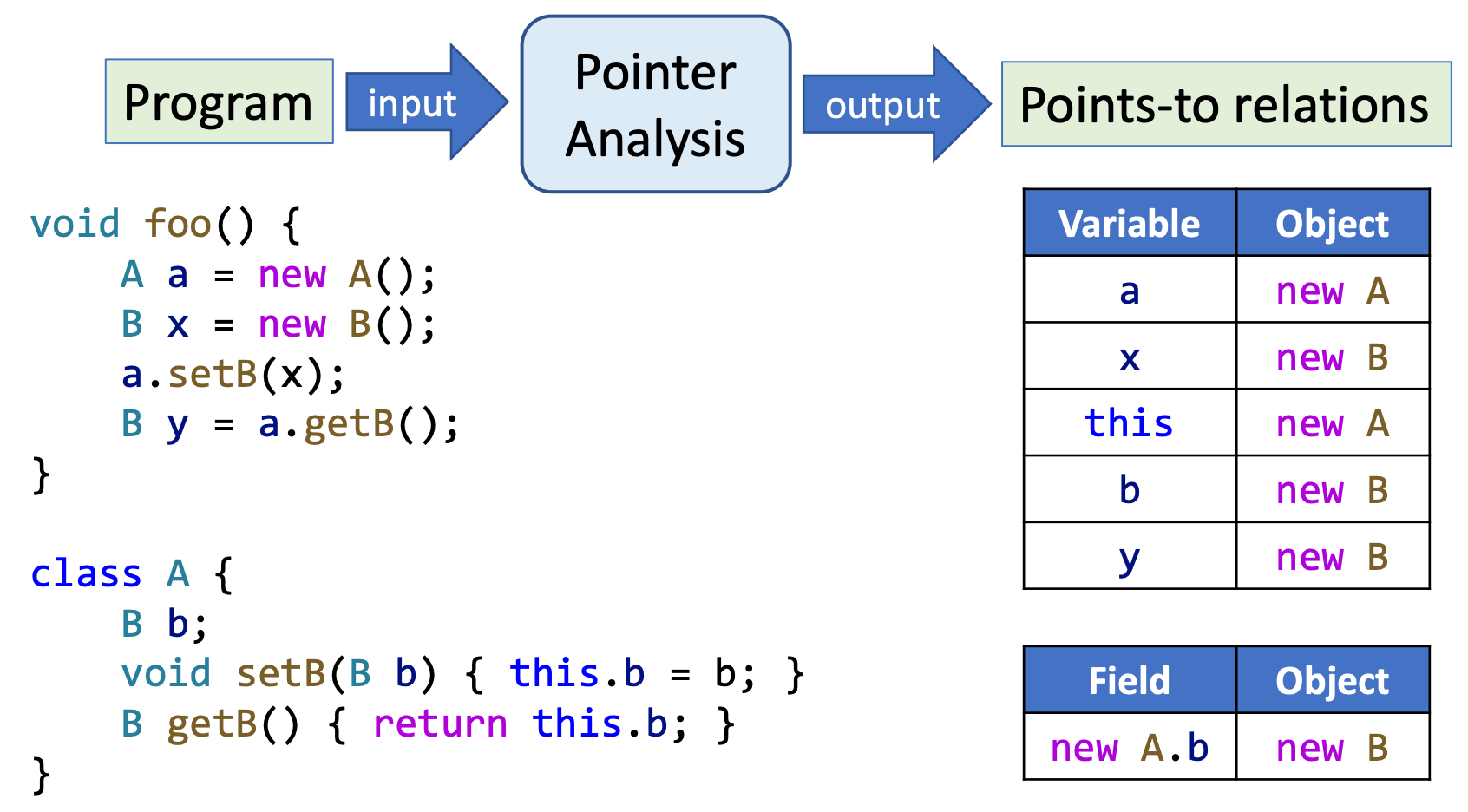
pta-example

影响指针分析的要素

指针分析是非常复杂的系统，许多因素都会影响其 精度和效率，标红的是本课程内容：

Key-Factors-PTA

1. 堆抽象

为了保证静态分析能够终止，对堆内存进行建模，把 动态分配的无限的具体对象 构建成 有限的抽象的对象

for(...){
  A a = new A(); // 每次迭代新建对象
}

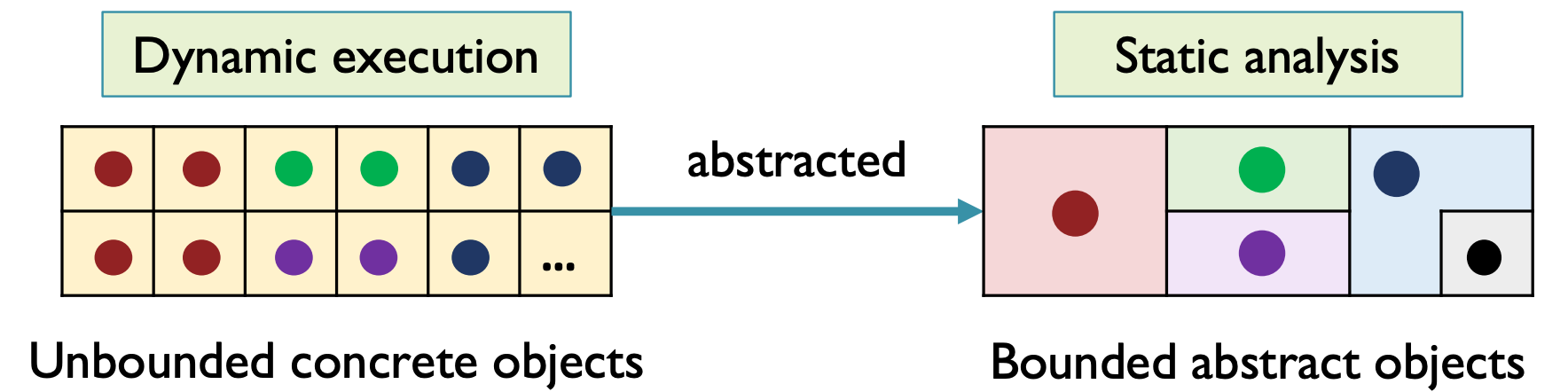
heap-abstract

堆抽象是一门十分复杂的学科，有无数的研究和方法，根据综述大概可分类为：

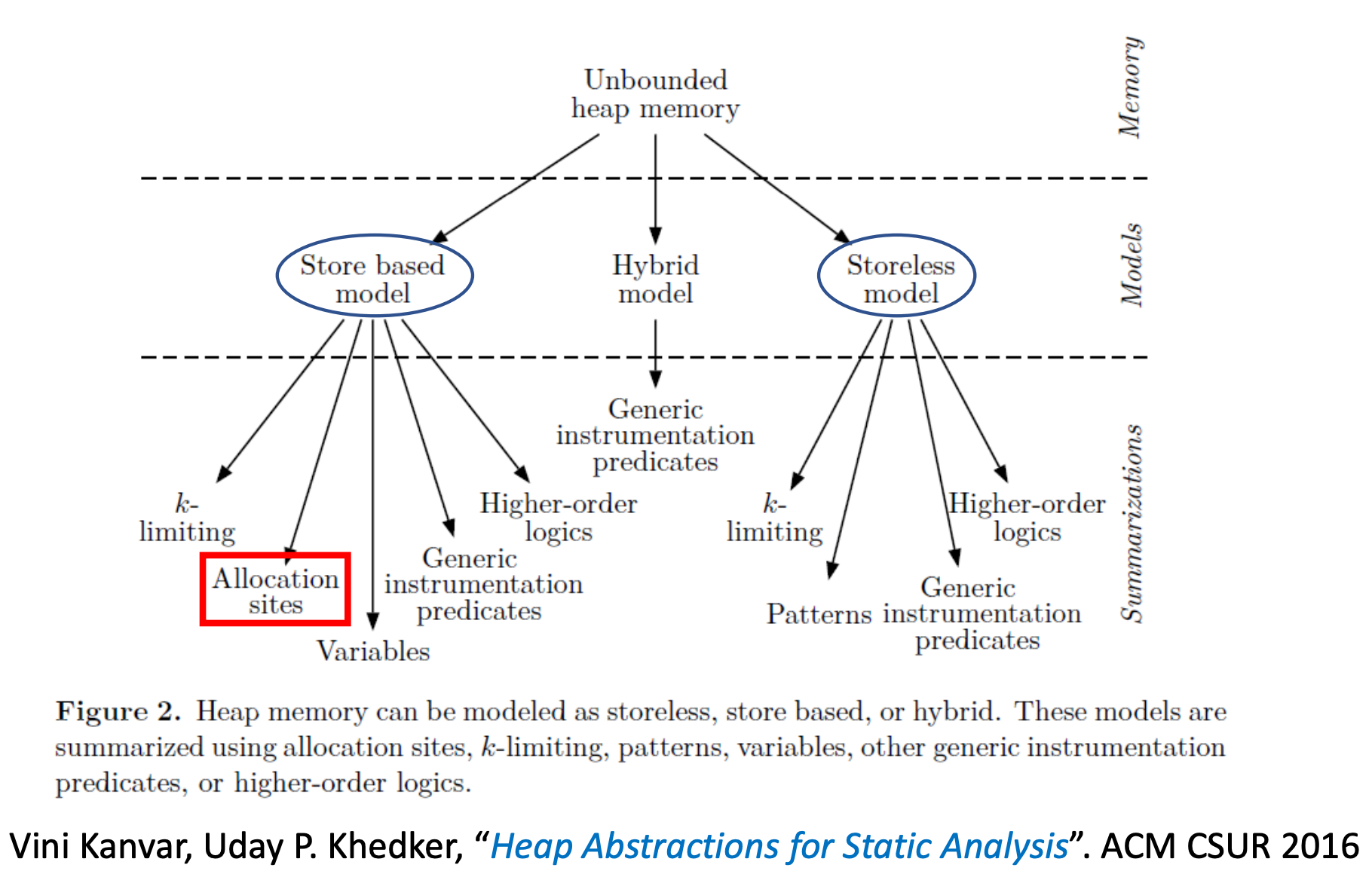
head-abs

本课程中，仅介绍最常用的 Allocation sites 堆抽象方法：

根据具体对象的 allocation site 对其建模
每个 allocation site 分配一个抽象对象，其代表所有在此处分配的具体对象

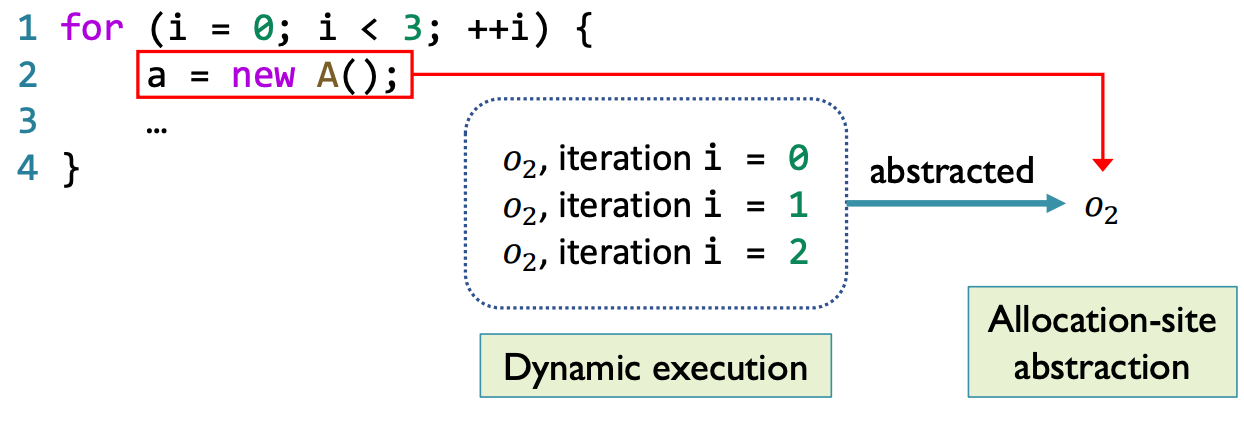
allocation-sites

在上图中，由于循环的存在，在迭代过程中会创建无数的具体对象，但由于对象的 allocation site 数量是固定的，因此抽象对象的数量也是固定的，在本例中为 1 个抽象对象。

2. 上下文敏感

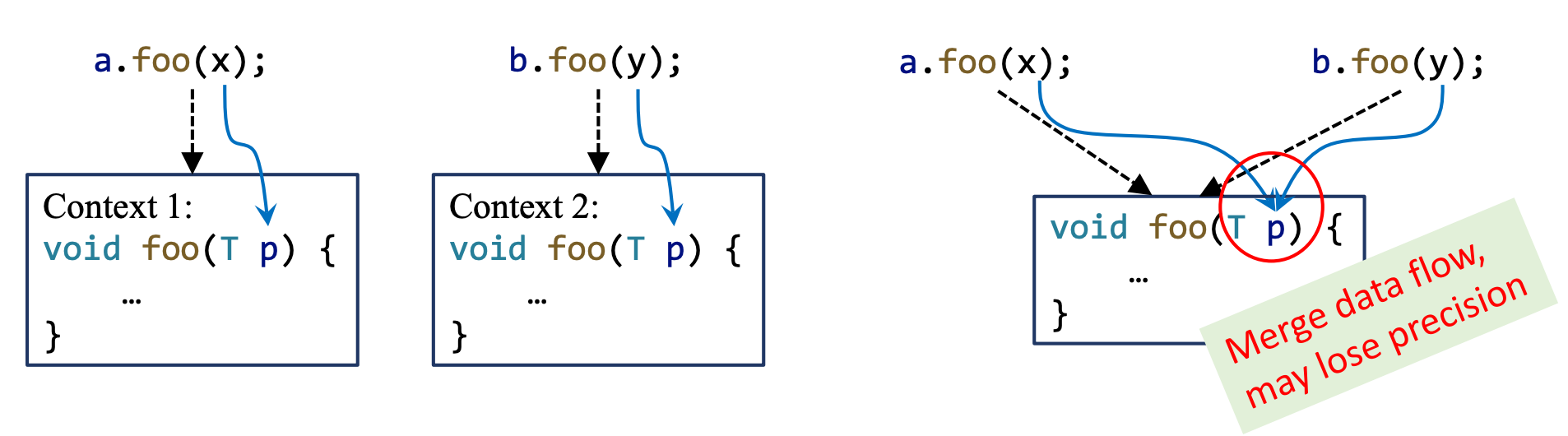
上下文敏感的分析中，对同一个方法的不同调用进行区分，对每一个上下文都分析一次目标方法，上下文敏感的分析可以有效的提升检测精度。
上下文不敏感的分析中，对同一个方法的不同调用做数据流的合并处理，只分析一次，可能丢失精度。

Context-Sensitivity

3. 流敏感

流敏感的分析是尊重语句的执行顺序的，程序中每个位置都维护了一个包含指向关系的 map

流不敏感的分析是忽视控制流的顺序的，整个程序只维护了一个包含指向关系的 map

flow-sensitive-vs-insensitive

4. 分析域

全程序分析：计算程序中所有指针的信息，服务所有可能的应用

需求驱动分析：只计算需要用到的指针的信息，服务特定的应用

指针分析关注的语句？

程序语言中存在很多类型的语句：

if else
for/while
break/continue
...

显然，上述的语句并不会影响指针的指向，因此我们只关注只关注 Pointer-Affecting Statements

JAVA 中的指针：

本地变量（local variable）e.g. x
静态字段（static field）e.g. C.f
实例字段（instance field）e.g. x.f
数组元素（array element）e.g. array[i]

在数组元素的指针分析中，忽略数组下标，把整个数组视作一个单独的 field，此时对数组元素的处理就与实例字段十分相似了。

array-point

处理静态字段的方式与处理本地变量相似，处理数组元素的方式与处理实例字段相似，因此在本课程中主要关注本地变量和实例字段的教学。

JAVA 中的 pointer-affecting statements：

创建 New x = new T()
赋值 Assign x = y
存储 Store x.f = y
加载 Load y = x.f
调用 Call r = x.k(a, …)
Static call： C.foo()
Special call：super.foo()/x.()/this.privateFoo()
Virtual call：x.foo() ——重点！

指针分析理论基础¶

指针分析：规则¶

首先，我们介绍一下相关的域（domain）和记法：

pta-domain

其中，$o_i$ 表示第 $i$ 行新建的对象，$P(O)$ 表示 $O$ 的幂集，$pt(p)$ 表示变量 $p$ 的指向的对象的集合。

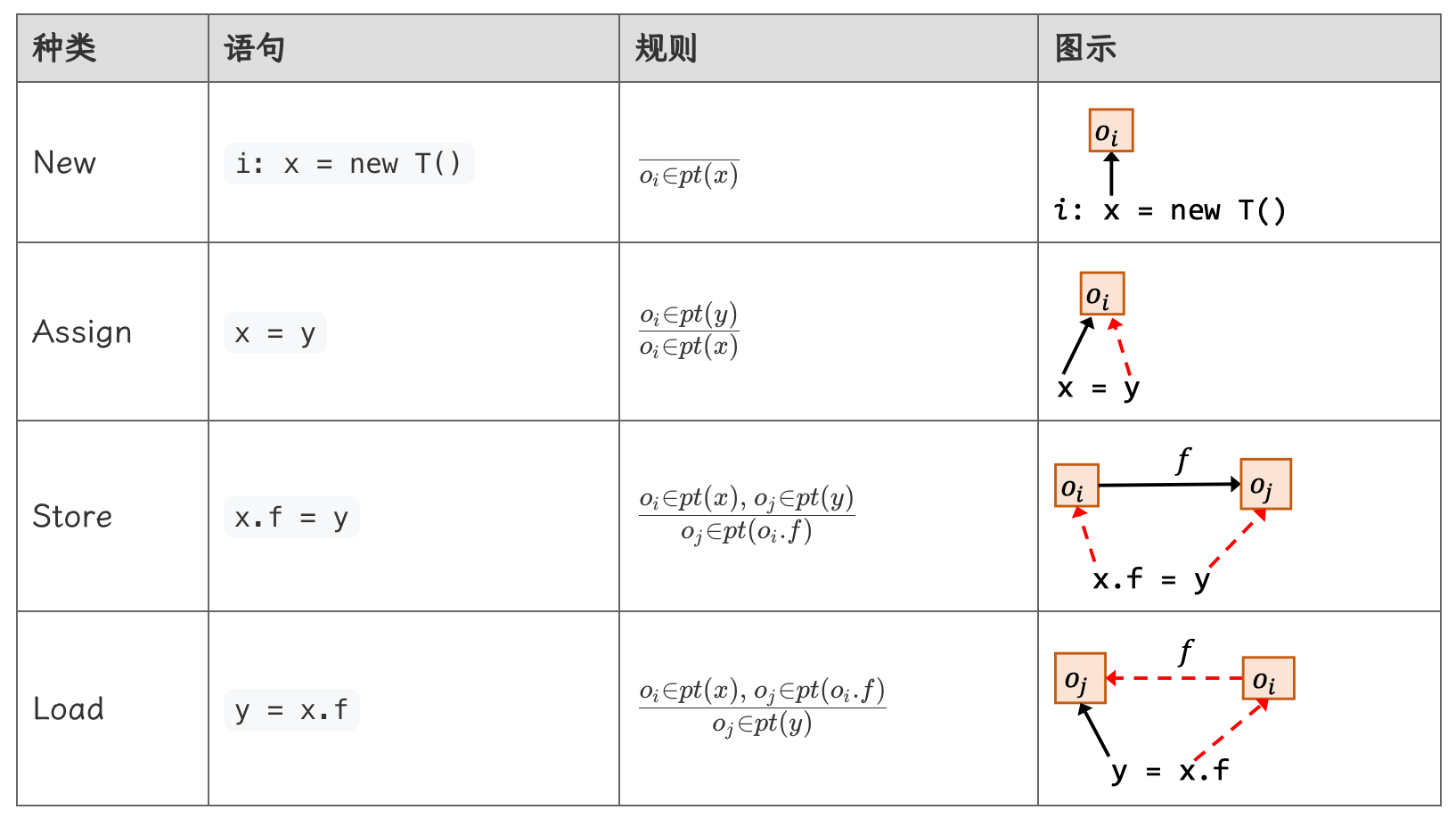
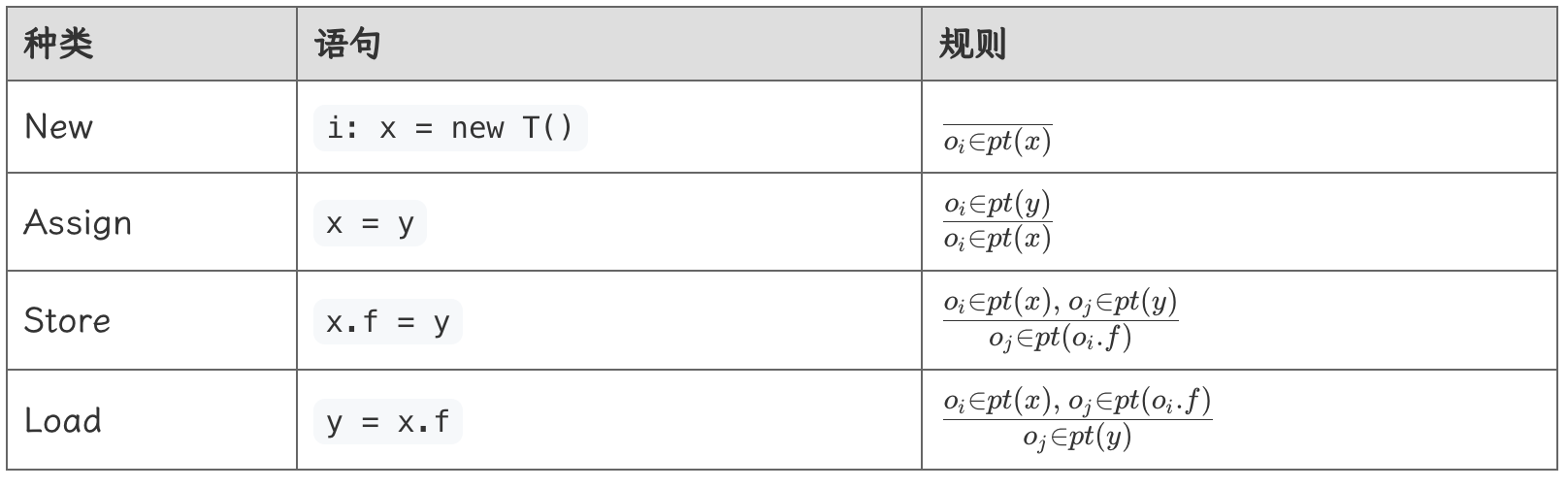
由于方法调用较为复杂，首先关注前四个语句的规则：

pta-role

规则部分，横线上方是前提（premise），下方是结论（conclusion）。

New：对应的规则的横线上方是空的，意味着当分析到 New 语句时，无条件得出横线下方的结论，也就是将 $o_i$ 无条件加入指向集合 $pt(x)$ 中，其含义为变量 $x$ 指向对象 $o_i$
Assign：当遇到赋值语句时，首先需要满足横线上方的前提，也就是 $y$ 变量指向某个对象，例如 $o_i$。随后执行横线下方的规则，由于将 $y$ 赋值给了 $x$，因此 $x$ 也要指向 $y$ 指向的对象，即让 $x$ 也指向 $o_i$
Store：个人认为本质上仍然是赋值，但赋值的对象是变量 $x$ 指向的对象（$e.g. o_i$）的域 $f$，即 $o_i.f$。
Load：类似。

如何实现指针分析¶

本质上来说，指针分析的过程，其实是在指针（variables & fields）之间传播（propagate）指向信息。

指针分析实现的关键是，如果 $pt(x)$ 改变了，应该将这种改变传播到 $x$ 关联的指针上。

图结构很适合这类分析，我们使用指针流图（pointer flow graph，简称 PFG）来表示程序中对象是如何在不同指针之间“流动”的，$pt(x)$ 需要被传播到图中 $x$ 的所有后继节点上。

PFG：

节点就是指针，即变量或对象的域。$Pointer = V ∪ (O × F)$
边。$Pointer × Pointer$。$x→y$ 的边表示指针 $x$ 指向的对象可能（may）会流动到指针 $y$。

PFG 的边需要根据中的程序语句和前面介绍的处理规则来添加：

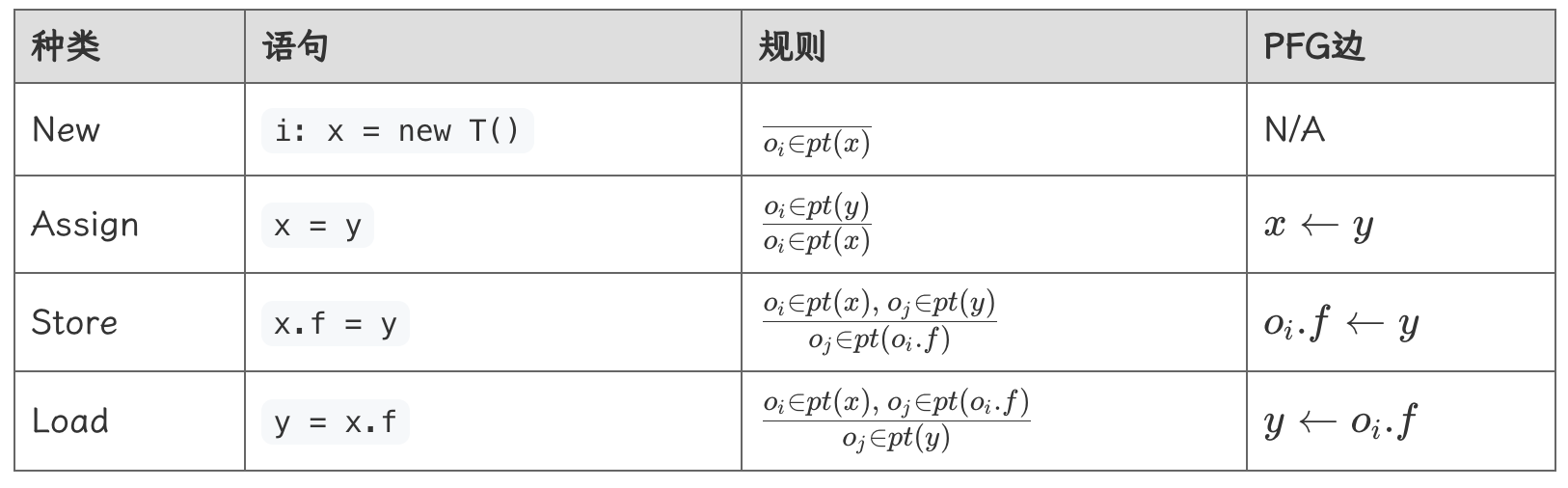
pta-edge-role

如下是一个指针分析的例子：

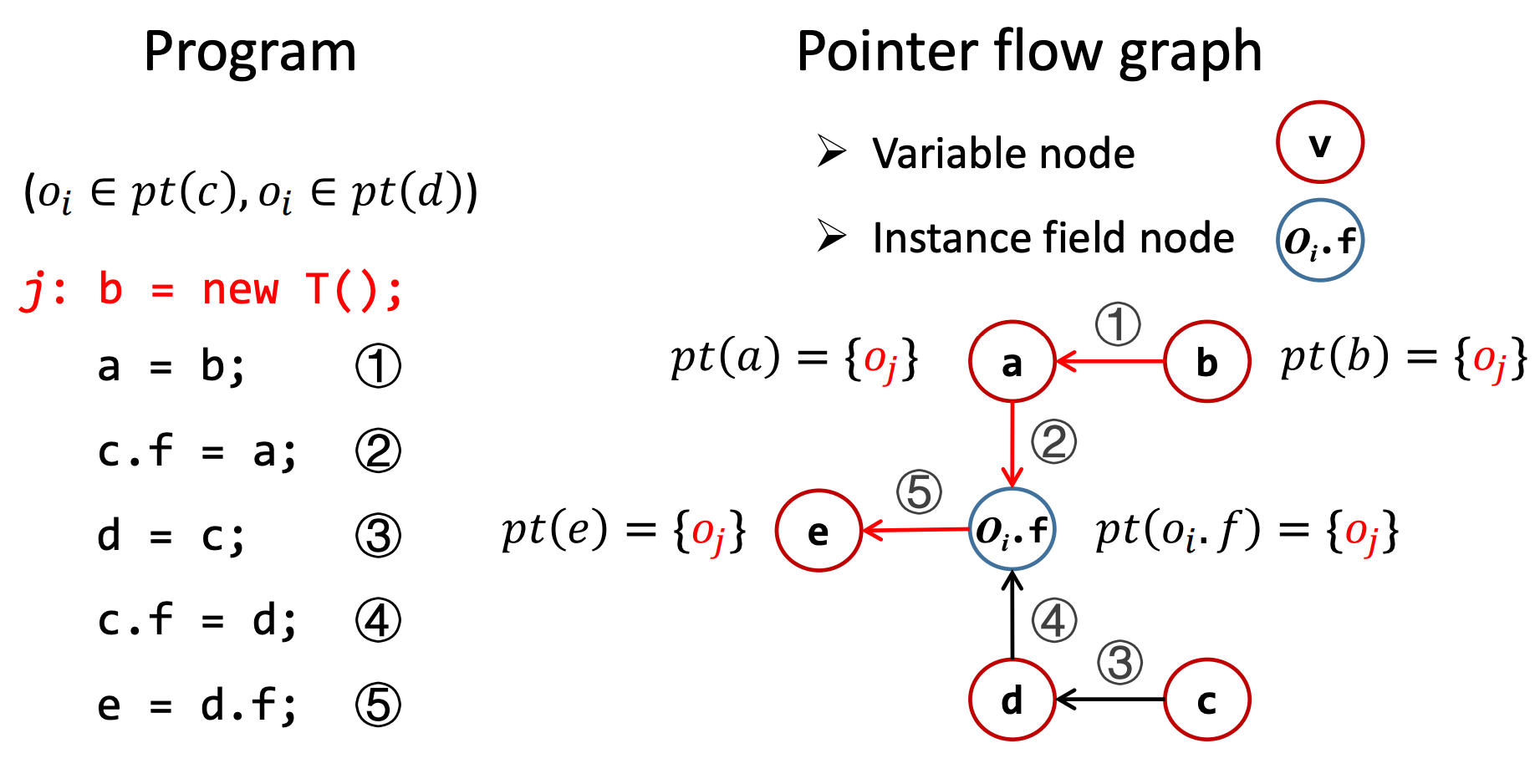
PFG-example

在构建完 PFG 之后，开始进行传播指针指向信息，由于语句 j: b = new T();，所以 $pt(b) = \{o_j\}$，又由于 PFG 中的边代表着指向对象的流动，即变量 $b$ 指向的对象，会流动到变量 $a$，因此变量 $a$ 也有可能指向变量 $\{o_j\}$，即 $pt(a) = \{o_j\}$。同理，对象的域 $o_i.f$ 和变量 $e$ 也有可能指向变量 $\{o_j\}$。

在上述的例子中，指针分析分为两个步骤：

首先构建 PFG
然后在 PFG 上传播指针指向信息

我们之所以可以构建 PFG，是因为首先假设了 $o_i ∈ pt(c), o_i ∈ pt(d)$，但实际上，该指向信息必须基于 PFG 才能获取。 当然，在传播指向信息时，又需要依赖 PFG。也就是说，上述两个步骤呈现互相依赖的关系，而不是简单的先后顺序。

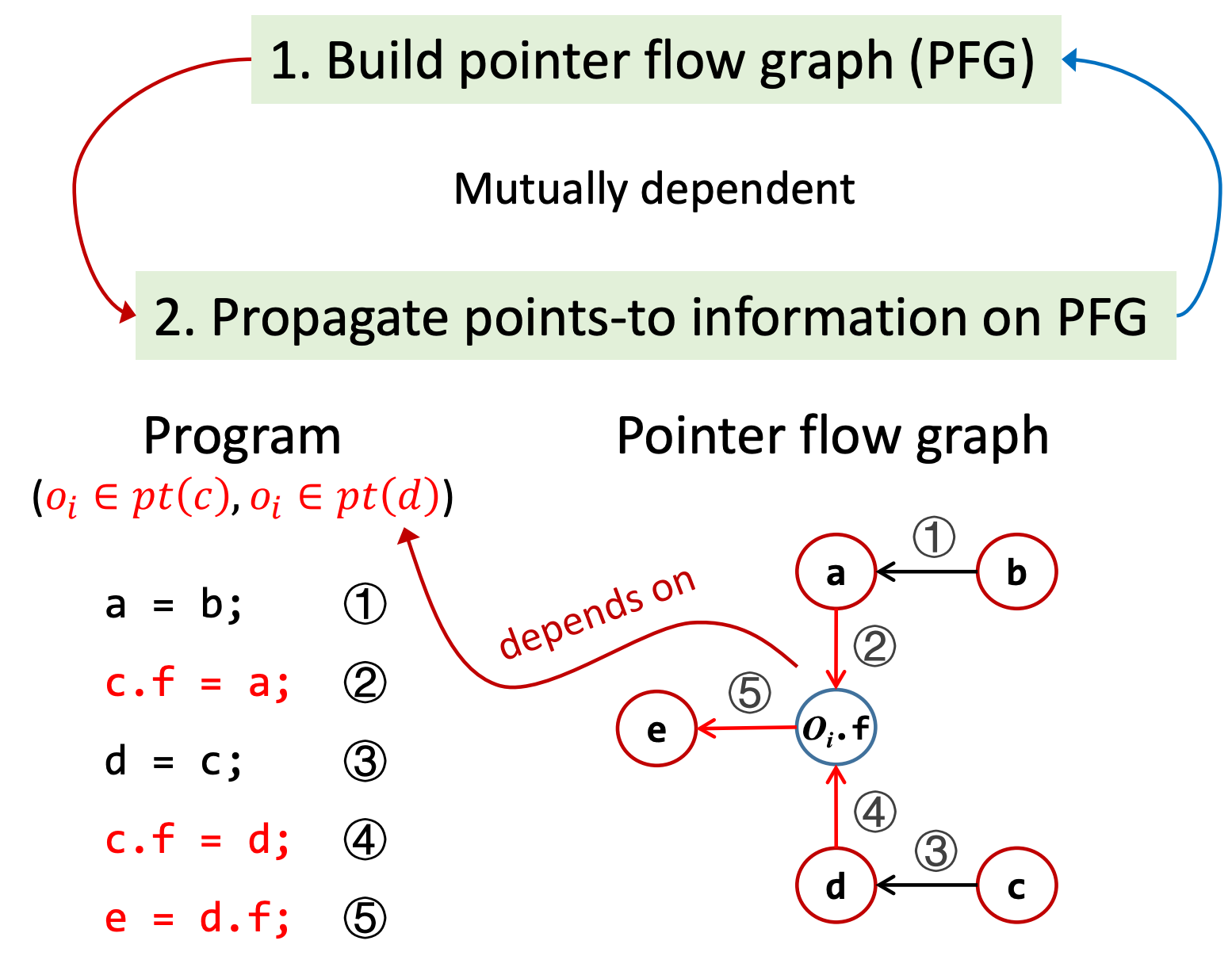
pfg-pta-cyclic-dependence

在构建 PFG 的过程中，$o_i.f$ 节点相关信息的构建依赖于指针的指向信息，例如在分析语句 ② c.f = a 时，根据规则，首先要知道变量 $c$ 指向的对象集，即 $pt(c)$。

总的来说，在指针分析的过程中，PFG 是会动态更新的，而不是先构建 PFG，再进行所谓的指针分析。

指针分析算法¶

pta-alg-without-mc

该算法输入为语句集合 $S$，由于是 流不敏感算法，在分析时并不关注语句的执行顺序。

初始化：WL, Work List 工作列表；PFG，pointer flow graph，指针流图。

WL 中包含了待处理的指向信息，其中每一项均为形如：$<n,pts>$ 的对，含义为指针 $n$ 和对象集合 $pts$，我们需要在后续的处理中，将 $pts$ 中的对象传播到 $pt(n)$ 中。通俗的说，就是让 $n$ 也指向 $pts$ 中的对象。

首先处理创建新对象的 New 语句，对于每一个 New 语句，将会在 PFG 中对应一个节点。我们将 $<x,\{o_i\}>$ 加入到 WL 中，在后续的处理中，我们需要让 $x$ 也需要指向 $pts$ 中的对象，并沿着 PFG 将 $pts$ 中的对象集合传播下去。
接着处理赋值语句 Assign，它将直接在 PFG 中的节点之间添加边 $y → x$，如果 $y$ 指向某个对象，那么 $x$ 也要指向该对象。在算法的设计中，我们通过将 $<x,pt(y)>$ 加入 WL 更新 $x$ 的指向的对象集合，让 $x$ 也指向 $y$ 指向的对象。（AddEdge 方法）。
处理完 New 和 Assign 语句后，已经在 WL 中加入了待处理的指向信息，接下来的算法 基于 WL 的循环，当 WL 为空时停止：
首先从 WL 中拿出一个待处理对，此处记为：$Processing <n,pts>$
基于 差分传播 思想，计算 $\Delta = pts -pt(n)$，由于我们当前正在处理指针 $n$，而 $pt(n)$ 中就是 $n$ 已经指向的对象，通过计算 $\Delta$，就可以避免重复处理已经指向的对象，而关注于 $pts$ 中新的对象。该步骤的作用就是节约时间，对正确性无影响。
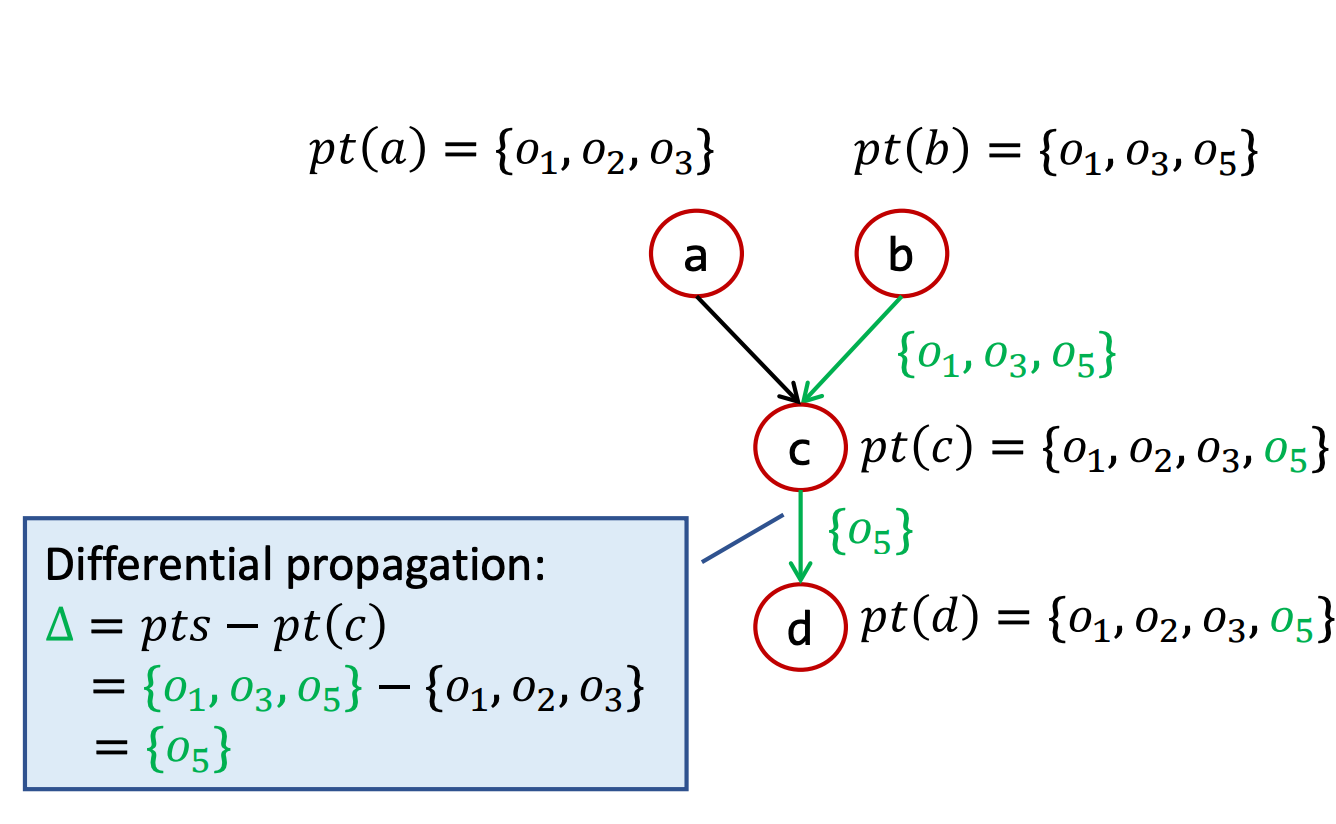
随后执行方法 $Propagate(n, \Delta)$ ，该函数首先将 $\Delta$ 中的对象加入 $pt(n)$ 中，也就是让 $n$ 指向 $\Delta$ 中的对象。随后，对于所有 $n$ 的后继边 $n → s$，将 $<s, \Delta>$ 加入 WL 中。

将 $<s, \Delta>$ 加入 WL 中就意味着后续循环的时候，将回让 $s$ 指向 $\Delta$ 中的对象，并继续向下传播。
由于 $n$ 有两种可能：① 变量，例如 $x$；② 实例字段，例如 $o_i.f$。当 $n$ 是变量时，由于 $n$ 指向了新的对象实例，那么对于 Store 和 Load 语句，也需要更新：
- Store 语句 $x.f = y$，对于 $\Delta$ 中的所有对象 $o_i ∈ \Delta$，需要让 $o_i.f$ 也指向 $y$ 指向的对象，因此添加边 $y → o_i.f$ ，此外，还要更新指向信息。（AddEdge 方法）
- Load 语句 $y = x.f$，同理，只是指向的方向不同。

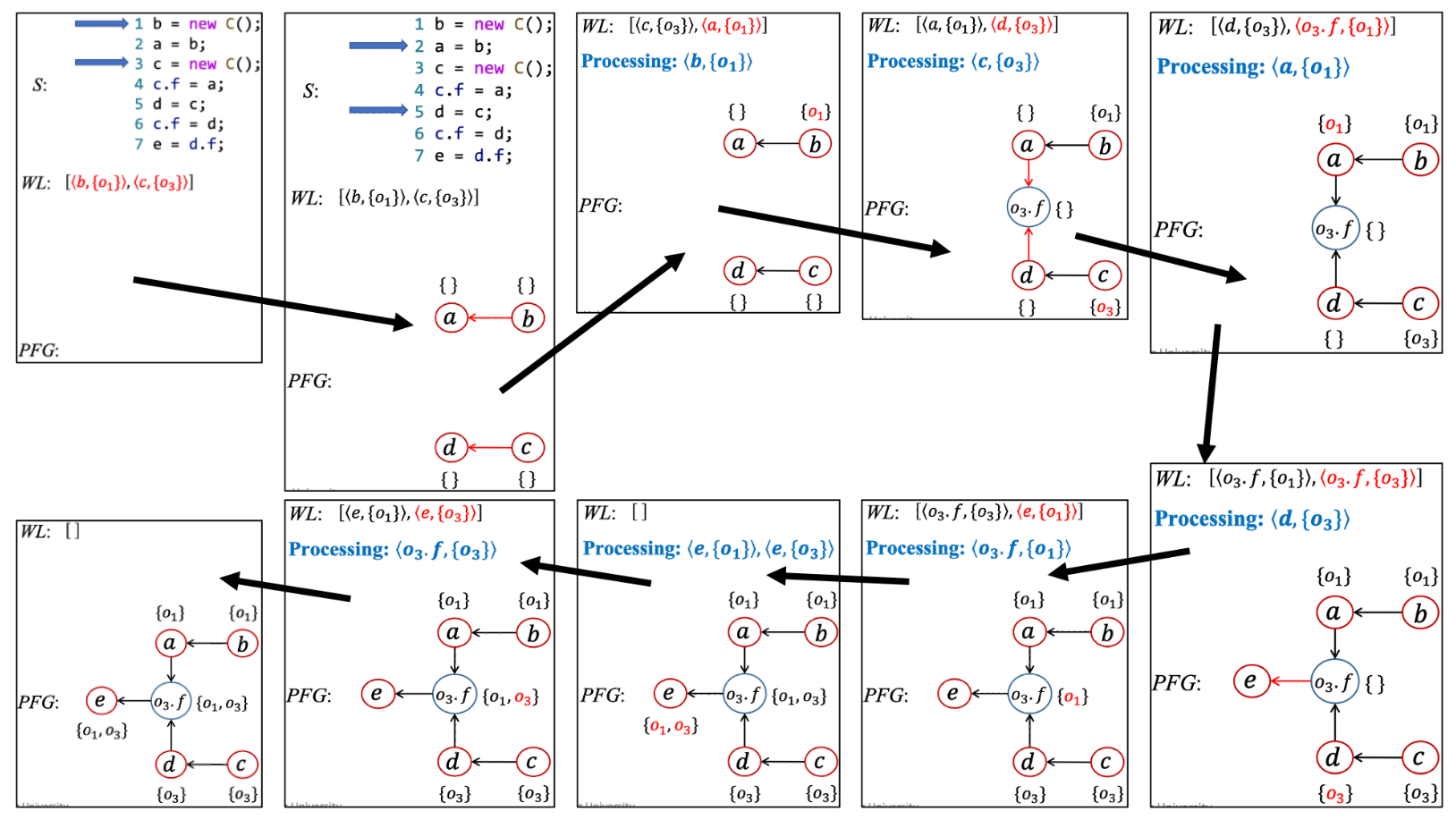
根据上述算法，在指针分析的过程中动态更新 PFG，具体例子如下：

pta-example-without-mc

指针分析：方法调用¶

在指针分析中引入函数调用实际上就是在进行 过程间指针分析，因此它依赖调用图（call graph）。我们之前介绍了基于 CHA 的调用图构建方法，然而这样构建出来的调用图精确度比较低。

我们将介绍基于指针分析同时构建调用图和指向关系的算法。由于指针分析中对象的创建是动态的，这种调用图构建方法又称作“on-the-fly call graph construction”。

一、规则

pta-edge-call-role

根据条件 $o_i ∈ pt(x)$，可知变量 $x$ 指向对象 $o_i$，通过 Dispatch 方法基于对象 $o_i$ 的类型定位到该对象所属类的方法 $m$。

对于一个方法，需要传递的指针共有三类：

对象自身，也就是 this：在 PFG 中，我们并不会在变量 $x$ 与 $m_{this}$ 之间添加边，而是 直接将变量 $x$ 所指的对象传播给 $m_{this}$ （即让指针 $m_{this}$ 也指向对象指针 $x$ 指向的对象。$o_i ∈ pt(x),o_i ∈ pt(m_{this})$），否则可能会增加许多不必要的虚假边（考虑一下 $x$ 可能指向多个对象，而对象所属类又具有多层继承关系的情况）。

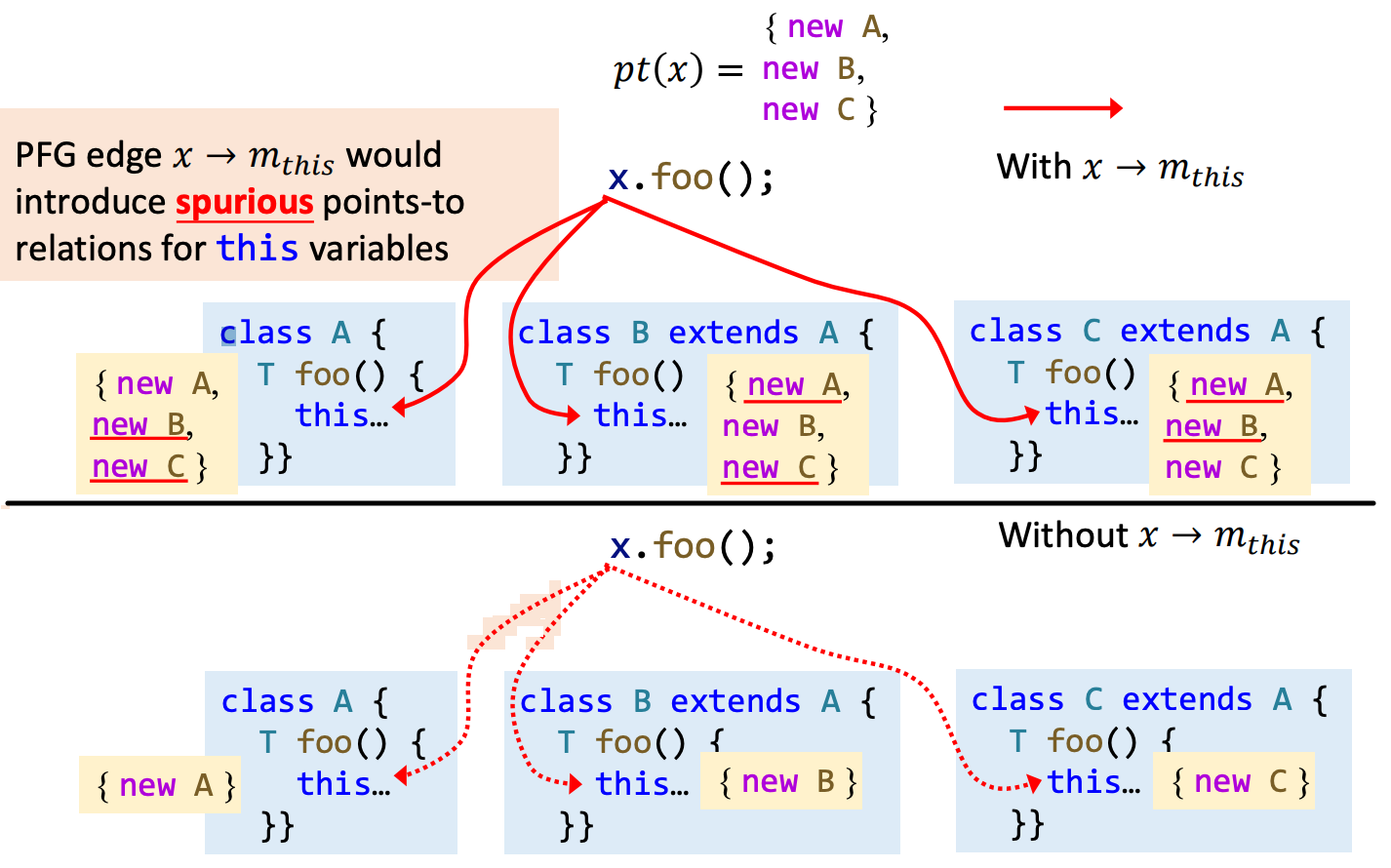
m-this

方法参数：在 PFG 中为形参和实参都新建一个节点，并 让实参指向形参（例如：a1 → p1）
方法返回值：在 PFG 中将返回值和调用语句的左值新建节点，并 让返回值指向调用语句左值（例如 ret → r）

func_pta_example

二、过程间指针分析

在上面定义的规则的基础上，我们来考虑过程间指针分析的算法。首先需要注意的是，指针分析与调用图构建是相辅相成、互相依赖的。我们在上一节中提到过，“构建 PFG”与“在 PFG 节点间传播指向关系信息”是互相依赖的，这里也是一样。

过程间指针分析从 main 方法开始，直到分析完所有可到达的方法。

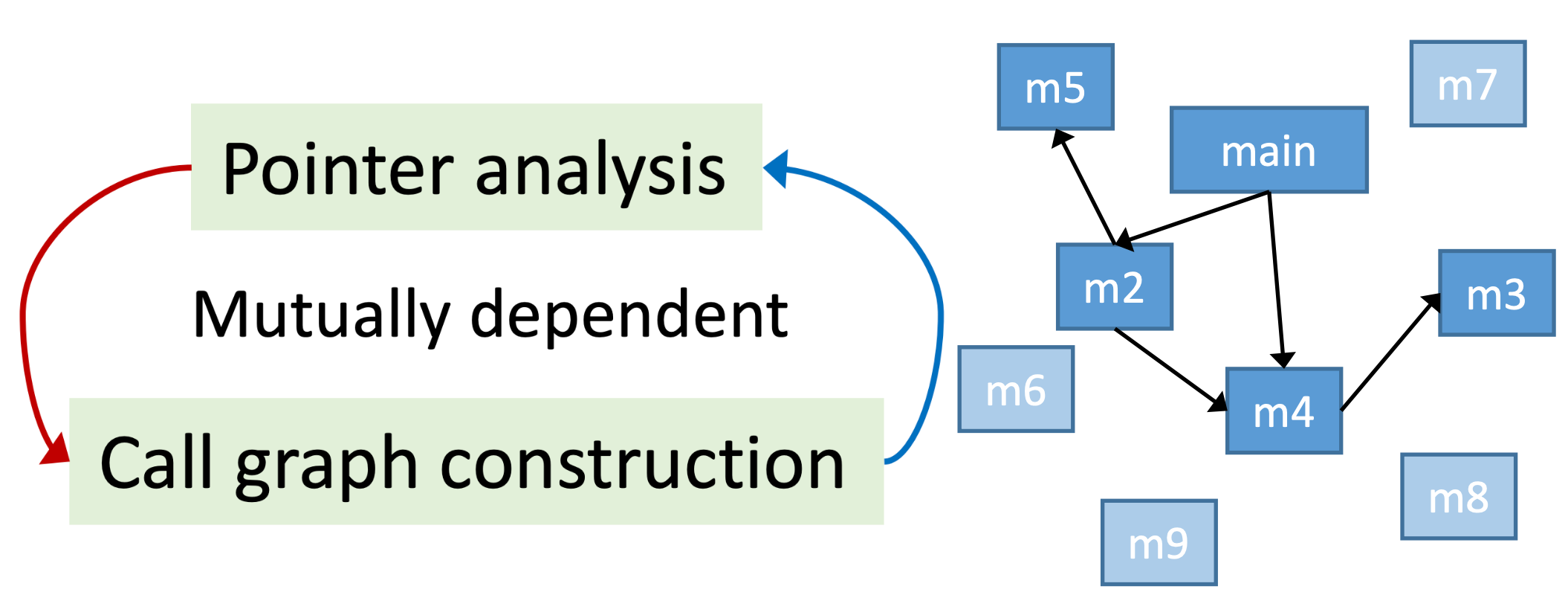
pta-cg-cycle-dep

三、过程间指针分析算法

在该算法中，将进行过程间指针分析，并同时生成 Call Graph，其算法如图所示：

pta-alg-with-mc

算法中的黄色部分是相比于过程间指针分析新增的部分。

初始化：算法输入由语句集合改为入口方法（e.g. main），新增三个空集合，分别是待分析的语句集合 S、已分析的方法 RM（用于避免重复分析）以及调用图 CG。
首先将调用 AddReachable 方法，说明该方法是可达的，若该方法未被分析过，则将其语句加入语句集合 S 中，在添加语句的过程中，如果发现有 New 语句或 Assign 语句，则做相应处理。
最后在传播过程中若 n 为变量，则会调用 ProcessCall 方法，该方法用于处理函数调用。
首先通过 Dispatch 方法找到实际调用的方法，使用变量 m 表示，并将 x 传播到 m，即让 m 指向 o，即算法中的 $add <m_{this},\{o_i\}> to \ WL$
更新 CG，设当前调用的语句位置为 $l$，在 CG 中新增边 $l → m$，同时扩大可达的方法范围（即此时将方法 m 认为是可达的，所谓可达就是程序执行的过程中会调用该方法，即它不是死方法）。
如同我们上面所说的，将参数和返回值按规则在 PFG 上添加边。

如此，即可完成指针分析，过程间指针分析算法最终的输出有两个：指向关系集合与调用图。

pta-example-with-mc

上下文敏感指针分析¶

虽然指针分析本身已经比 CHA 精确很多，但是前面我们学习的指针分析是上下文不敏感的，相对于上下文敏感的指针分析来说，会有一些 false positives。

谭添老师提到，上下文敏感分析是目前 Java 指针分析中最有效的分析方式。

void main() {
    Number n1, n2, x, y;
    n1 = new One();
    n2 = new Two();
    x = id(n1);
    y = id(n2);
    int i = x.get();
}
Number id(Number n) {
    return n;
}
interface Number { int get(); }
class One implements Number { public int get() { return 1; }}
class Two implements Number { public int get() { return 2; }}

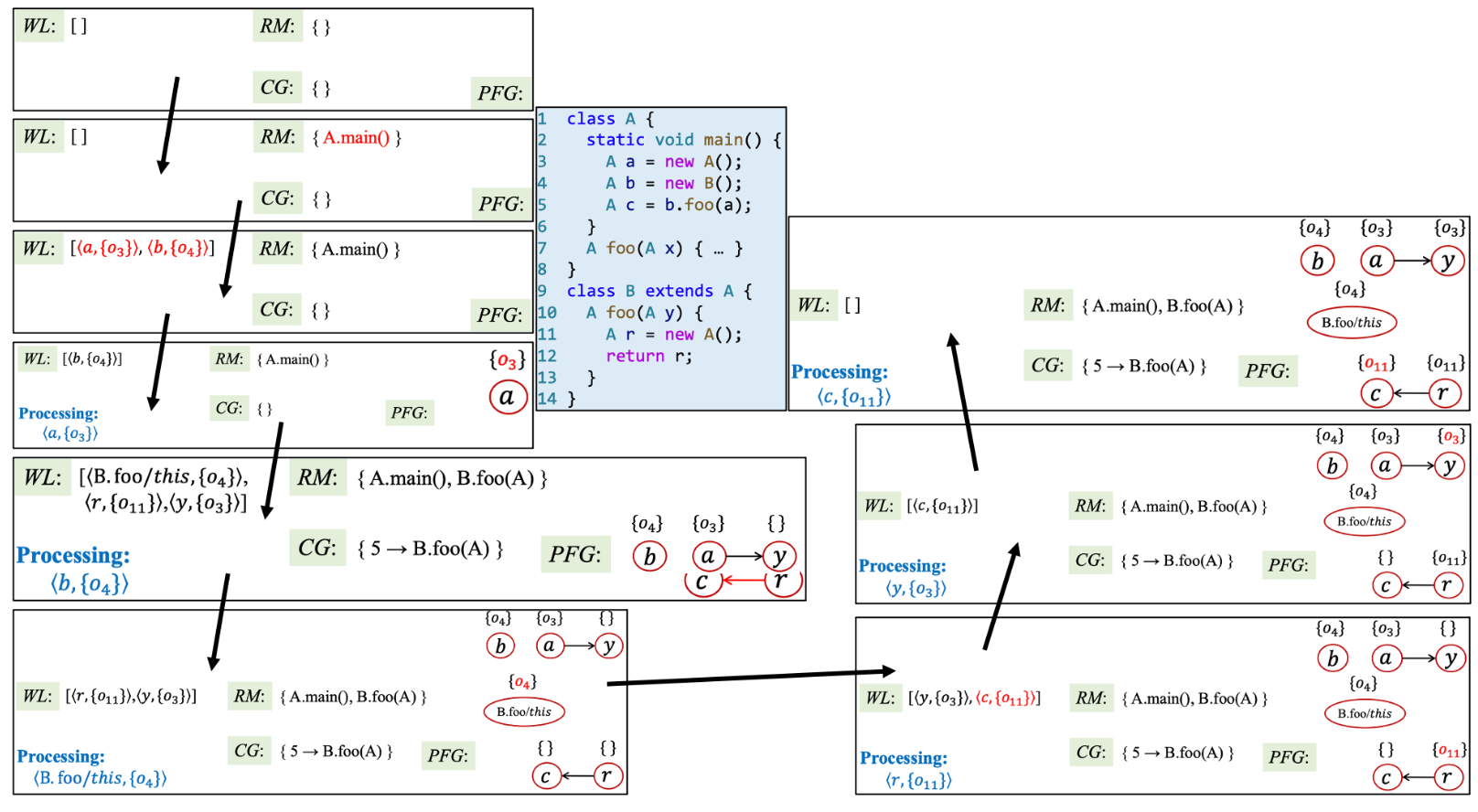
对于上述例子来说，上下文不敏感的指针分析将构建出图（1）PFG，如果在此基础上进行常量传播，变量 $i$ 的结果将是 NAC，因为它可能是 1 或 2。然而，事实上该程序真正执行时，变量 $i$ 只可能是 1，也就是变量 $x$ 只可能指向对象 $o_1$。

该 PFG 如何构建？

首先分析 New 语句时，构建节点 $n_1$ 和 $n_2$，分别指向对象 $o_1$ 和 $o_2$
当调用 id(n1) 方法时，在 PFG 中为实参和形参添加边，即 $n1 → n$，并传播对象，即 $pt(n) = \{o_1\}$。接着，在 PFG 中为调用接受变量和返回值之间添加边，即 $n → x$，并传播对象，$pt(x) = \{o_1\}$
同理，当调用 id(n2) 方法时，添加边 $n2 → n$，传播对象，此时 $pt(n) = \{o_1, o_2\}$。添加边即 $n → y$，并传播对象，，此时 $pt(y) = \{o_1, o_2\}$
此时，误报出现。

上下文敏感的指针分析时，误报消失，，变量 $i$ 结果将是 1，因为变量 $x$ 只指向对象 $o_1$。

cs-is-pfg

总的来看，上下文不敏感（context insensitivity，简称 C.I.）分析的不精确性主要体现在：

在动态执行过程中，一个方法可能在不同的调用上下文（calling contexts）中被调用多次。
在不同的调用上下文中，方法中的变量可能指向不同的对象。
在 C.I.指针分析中，不同上下文中的对象通过返回值或方法副作用被混在一起传播到程序各处，导致了虚假数据流。

上下文敏感（context sensitivity，简称 C.S.）分析通过区分不同上下文中的不同数据流来对调用上下文进行建模，从而提升准确性。

一、Call-Site Sensitivity

最经典的上下文敏感处理策略是 call-site sensitivity，它将每个方法的上下文表示为由 call sites 组成的链（可能包括方法的 call site，caller 的 call site，甚至 caller 的 caller 的 call site 等），对程序动态运行时的调用栈进行抽象。

例如，对于下面这一小段代码，在 call-site sensitivity 策略下，id(Number)方法有两个不同的上下文[1]和[2]：

1 x = id(n1);
2 y = id(n2);
3 int i = x.get();
4
5 Number id(Number n) {
6     return n;
7 }

在后续会更详细的介绍上下文敏感处理策略。

二、Cloning-Based Context Sensitivity

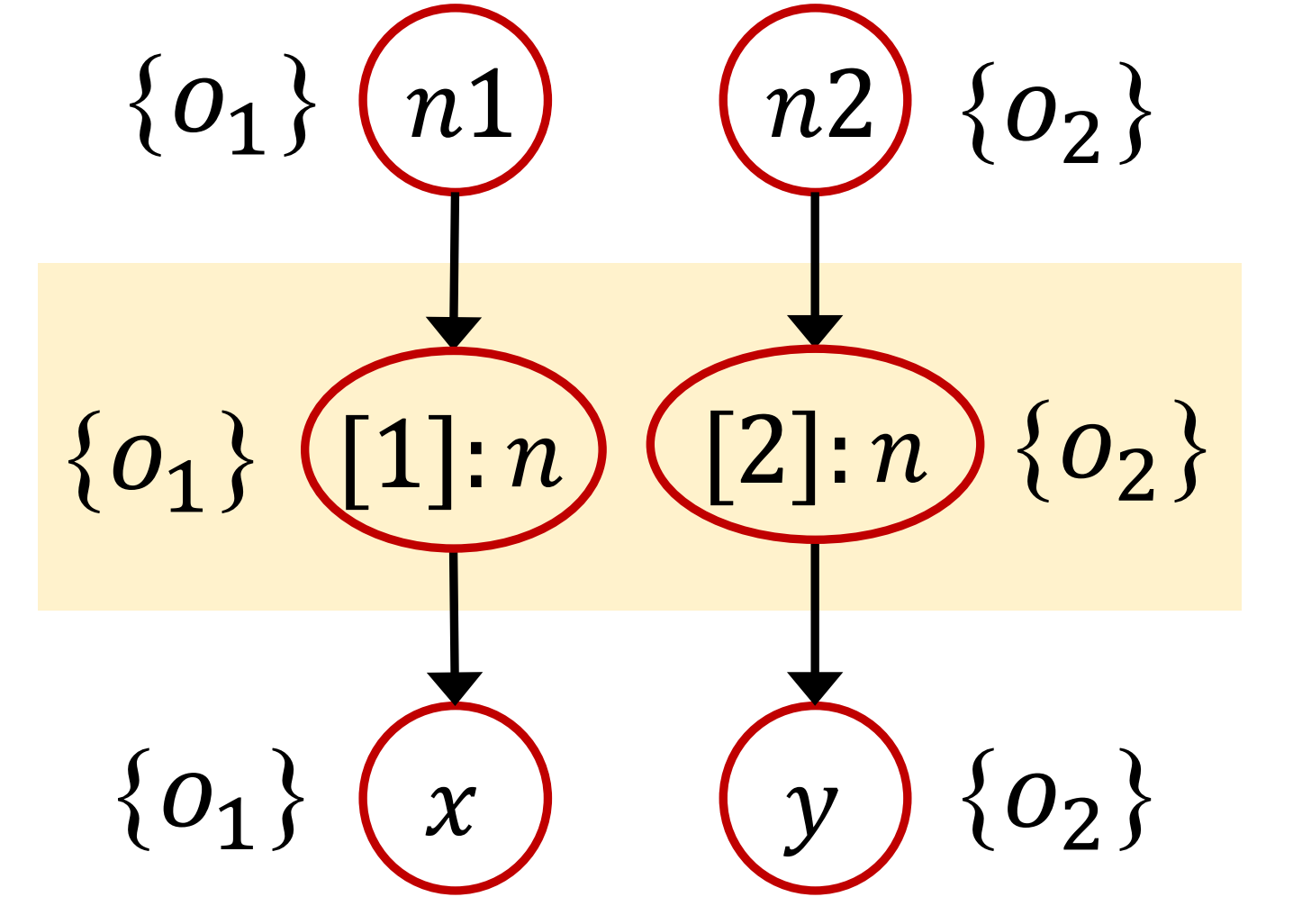
另外，一种最直观的上下文敏感实现方式是“cloning-based context sensitivity”，每个方法和变量都会带有一个或多个上下文。针对代码中的一个方法或变量，我们仿佛是为每个上下文克隆了一个该方法或变量，从而将它们区分开来。上述代码相应的 PFG 如下图所示：

Cloning-Based-Context-Sensitivity

三、Context-Sensitive Heap

面向对象的程序是 heap-intensive 的。因此，为了提高准确性，我们也要对堆抽象（heap abstraction）做上下文敏感处理——抽象对象将带有 heap context。在基于 allocation-site 的堆抽象基础上，上下文敏感的堆抽象将提供粒度更细的堆模型：

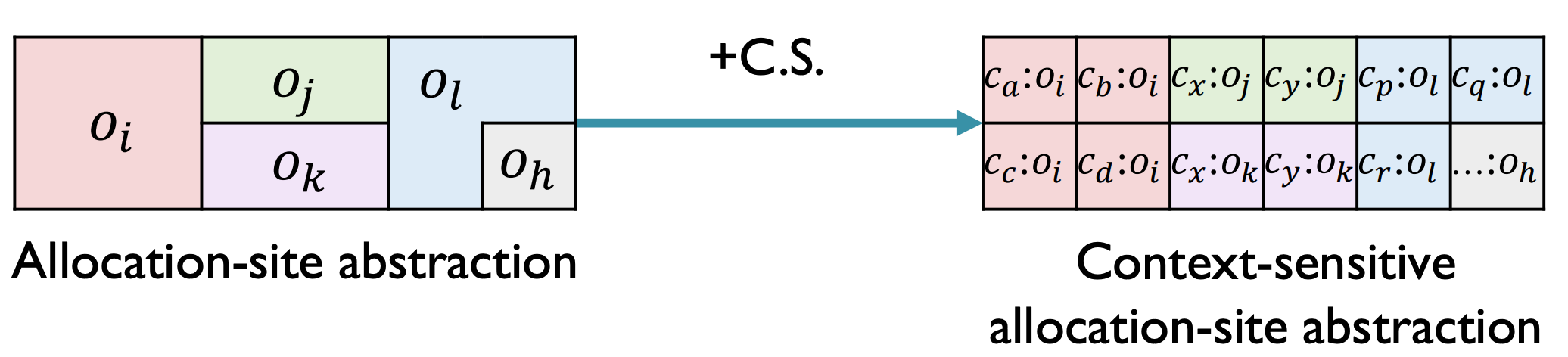
Context-Sensitive-Heap

为什么 C.S.的堆抽象能够提高准确性呢？这是因为（可以与前文描述的 C.I.的不精确性结合起来理解）：

在动态执行过程中，一个 allocation site 可能在不同的调用上下文中创建多个对象。
在同一个 site 创建的不同对象可能是由不同的数据流控制的——例如，将不同的值（值可能来自不同的方法调用）存储到对象的域中。

因此，在指针分析中，在没有 heap context 时，合并不同上下文的数据流到一个抽象对象可能导致准确度降低；将位于同一 allocation size 但不同上下文的对象区分开来才能提高准确度。

下面是一个对比的案例。

左侧表格展示的是对方法变量应用上下文敏感处理，但不对堆进行上下文敏感处理的指针分析结果；

右侧展示的是对方法变量和堆都进行上下文敏感处理的指针分析结果，可以看出，后者比前者更精准：

heap-example

另外，同时对方法变量和堆进行上下文敏感处理才能最大程度地提高精确度，只处理后者不处理前者同样会导致精确度降低：

heap-example2

四、规则

pta-sensitive-role

前四类语句规则与非上下文敏感的规则一致，唯一的不同就是上下文前缀。

例如：对于 Assign 语句 x=y，其规则为，上下文 c 中的指针 y 指向的对象，也需要让上下文 c 中的指针 x 指向（但不同的上下文之间互不影响。

方法调用语句新增了 Select 函数，用于为目标方法 m 根据 call site $l$ 处的信息选取对应的上下文，其中$c$ 是 caller 的上下文， $c^t$ 是 callee 的上下文。

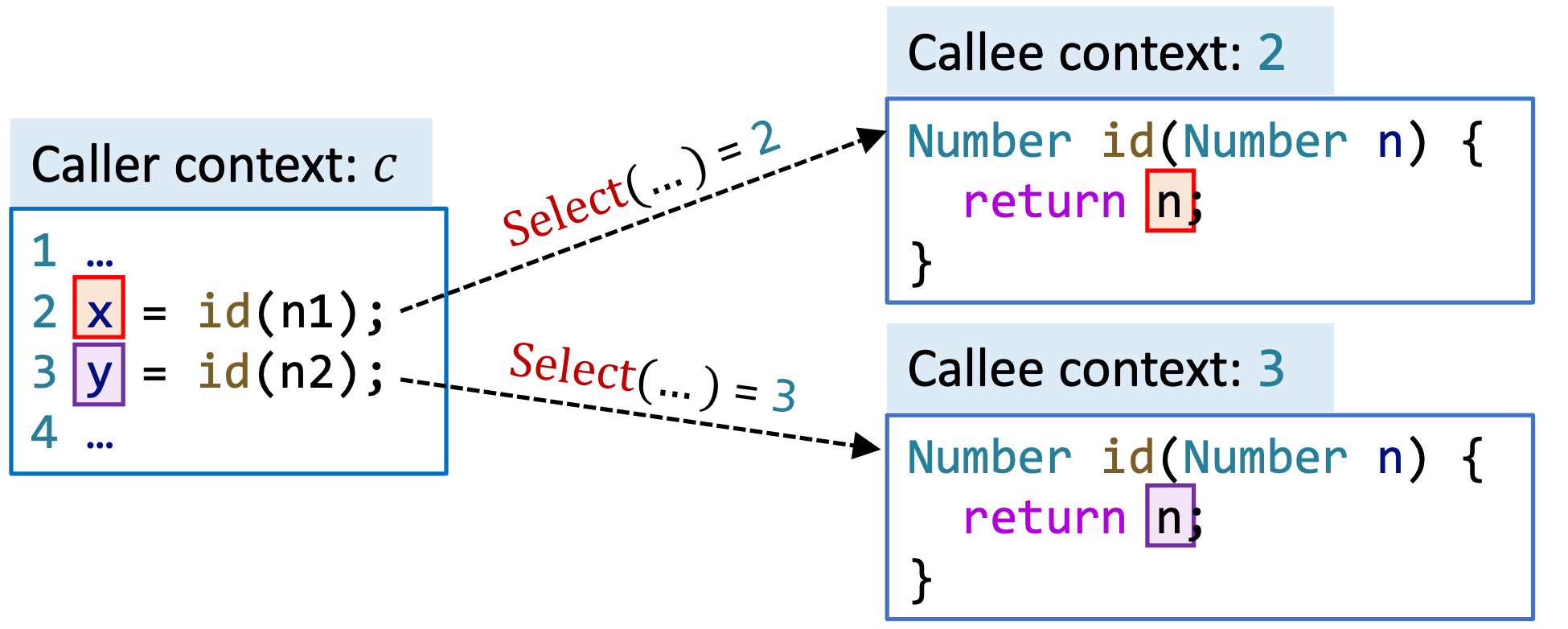
select

五、算法

pta-alg-with-mc-sensitive

C.S.的算法只是多了上下文限定（类似 $c:$ 这样的部分）和 $Select$ 函数。两个底层函数 Propagate 和 AddEdge 则在两个算法中完全相同——事实上，它俩从过程内 C.I.指针分析开始就没变过。

我们将在后续讲解 $Select$ 函数在不同策略下的具体实现。

六、上下文敏感变体（Context Sensitivity Variants）

在本节最开头，介绍了 Call-site sensitivity，但其实存在很多的敏感策略：

Call-site sensitivity
Object sensitivity
Type sensitivity
……

在学习这些处理方法之前，再看一下 $Select$ 函数的详细定义：

\[ c^t = Select(c,l,c':o_i) \]

其参数分别为：

caller context
call site
receiver object with heap context

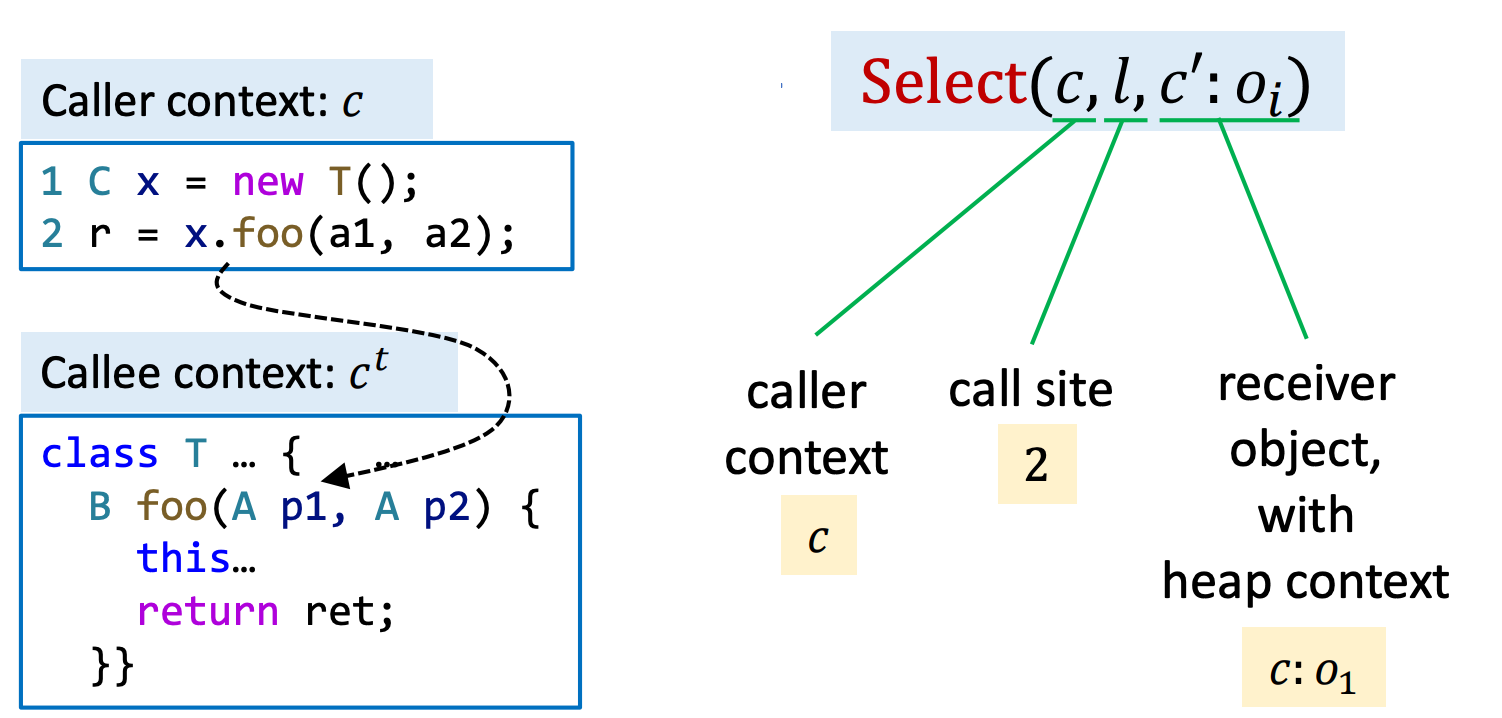
select-example2

在图例中，当执行第二行的方法调用时，其 Select 的结果如图右所示。

现在，可以认为 上下文非敏感是上下文敏感的一种特殊方式，即 $Select_(\_,\_,\_) = [\ ]$，也就是说 Select 函数始终返回空上下文（无上下文）。

Select 函数的三个参数并不是全是必须的，根据 C.S. 策略选择的不同，需要不同的参数。

6.1 Call-Site Sensitivity（K-CFA）

Call-site sensitivity 由 Olin Shivers 于 1991 年在他的博士论文Control-Flow Analysis of Higher-Order Languages中提出，CFA 的命名正是来源于该论文的缩写。

其思想是，每个上下文都是一个 call sites 列表（调用链），在方法调用时，将 call site 加入到 caller context 中，作为 callee context，实质上就是调用栈的抽象。其 Select 函数为

\[ Select(𝒄,𝒍,\_) = [𝑙' , … , 𝑙'',l] \ where \ 𝑐' = [𝑙' , … , 𝑙'' ] \]

因为上下文形如一个字符串，因此 call-site sensitivity 也叫做 call-string sensitivity，或者 K-CFA。

k-CFA 全称是 k-Limiting Context Abstraction，顾名思义，就是要限制上下文的长度。

Call-site sensitivity 的特性导致这样产生的上下文可能会非常长，比如递归的情况。一方面，我们要确保指针分析能够终止；另一方面，我们不希望上下文过长，也没必要过长。

k-cfa-limit-example

因此，我们为上下文长度设置一个上界 $k$——每个上下文只包括最新的 $k$ 个 call sites，更早的就丢掉。

实践中，$k$通常小于 3。另外，方法上下文和堆上下文可能采用不同的 $k$。

K-CFA 策略只需要使用 Select 方法的前两个参数，即：

caller context
call site：使用代码所处的行数代表。

实践中，k 通常取 1 或 2，下述是 k = 1 的例子：

ci-vs-1-call-site

6.2 Object Sensitivity

OK，接下来是第二种 C.S.处理方式：对象敏感性。这种处理方式在 2002 年的一篇论文Parameterized Object Sensitivity for Points-to Analysis for Java被提出，思路与前一种截然不同——用抽象对象（由对象 allocation sites 表示）列表来构成上下文，而非 call sites 构成。在方法调用时，将接收者对象和它的 heap context 作为 callee context。

其 Select 函数为：

\[ Select(\_,\_,c':o_i) = [o_j , … , o_k,o_i] \ where \ 𝑐' = [o_j , … , o_k ] \]

由于抽象对象由 allocation sites 表示，因此这种处理方式也叫做 allocation-site sensitivity。正是我们之前介绍的处理方式。

我们直接来看一个 1-CFA 和 1-object 对比的例子吧：

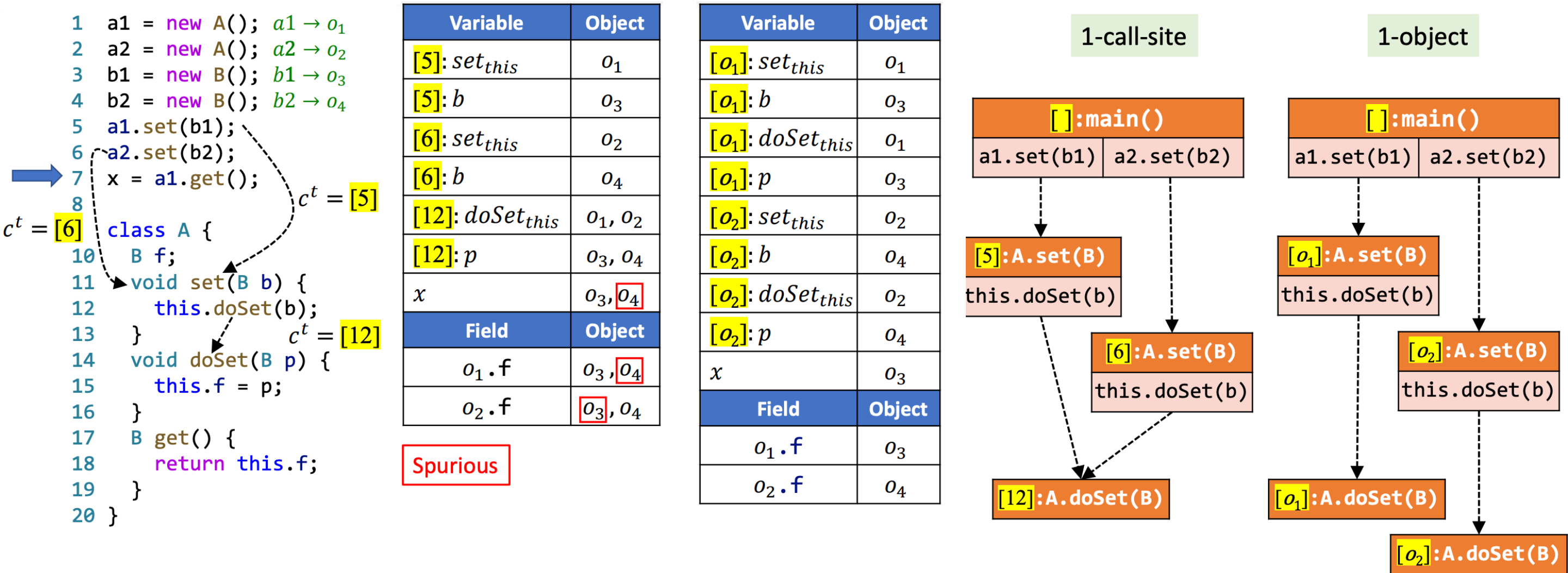
1-cfa-vs-1-object-example

在这个例子中，似乎 object sensitivity 更为准确。Object sensitivity 其实模拟的就是 Java 语言运行时的动态处理过程。具体到这个例子而言，不同的上下文都可能流经 call-site [12]，然而 1-CFA 导致历史上下文被丢掉了，准确度自然下降。增加 k-CFA 的 *k*可以缓解问题，但是并不能完全解决——只要类似的调用层数比 *k*大，这样的问题都会出现。

然而，object sensitivity 一定比 call-site sensitivity 更准确吗？不见得。用 object sensitivity 来处理一下上一小节中的那个例子，将结果与 call-site sensitivity 的结果做对比，可以发现，这次反而 object sensitivity 是不准确的那个：

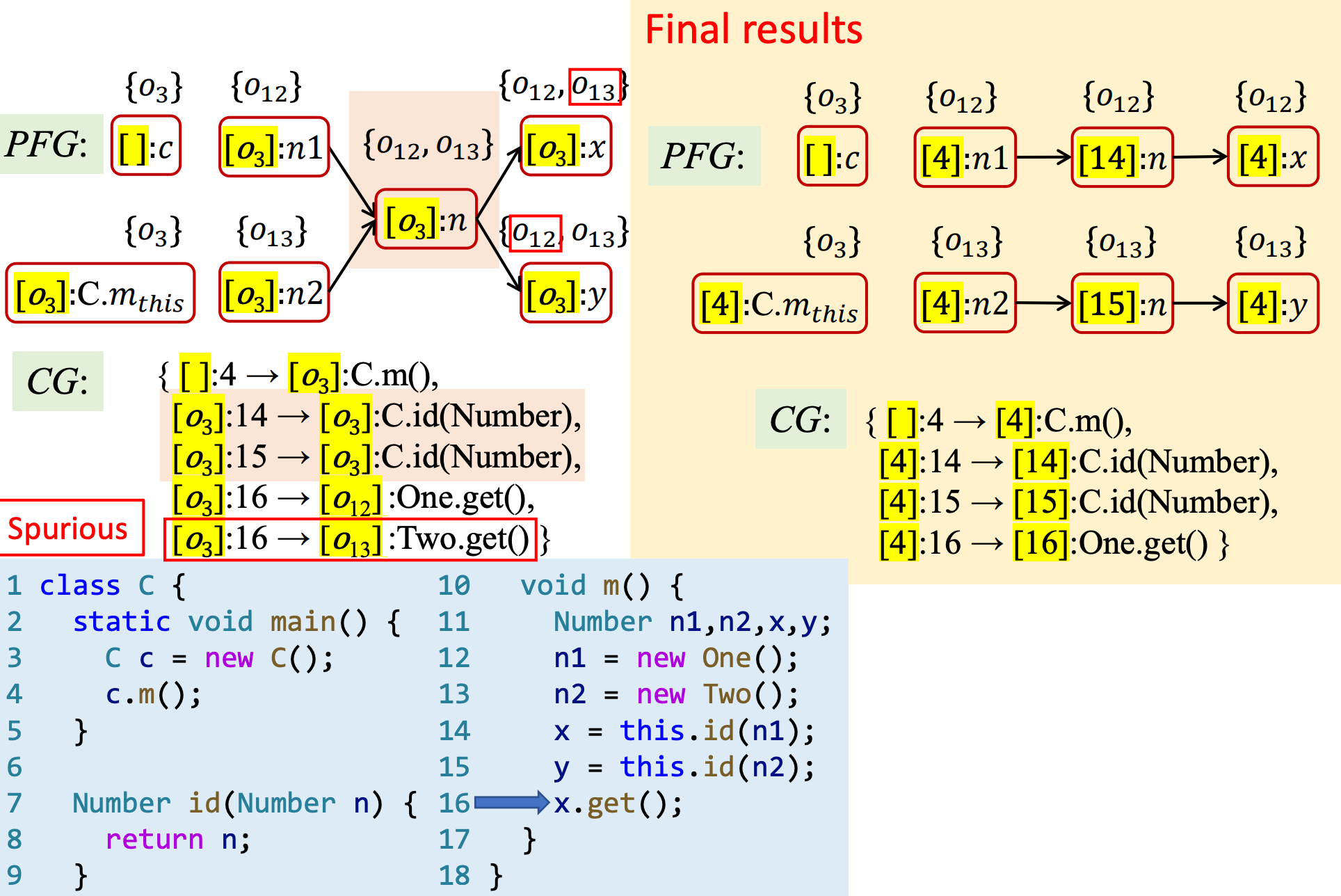
1-cfa-vs-1-object-example2

理论上，call-site sensitivity 和 object sensitivity 的准确性是不可比较的。

实践中，在处理 OOP 时，object sensitivityt 一般比 call-site sensitivity 的效果更好（具体到个例则另说）。

6.3 Type Sensitivity

第三种 C.S.处理方式是类型敏感性。从名字上我们就大概能猜出来它的思路，甚至能够猜到它的准确性可能会比 object sensitivity 低一些，但是效率会高一些。所谓类型敏感性，就是使用包含 allocation site 的“类型”和堆上下文作为 callee object。

其 Select 函数如下：

\[ Select(\_,\_,c':o_i) = [𝑙' , … , 𝑙'',InType(o_i)] \ where \ 𝑐' = [𝑙' , … , 𝑙'' ] \]

这种处理方式在 2011 年的一篇论文Pick YourContexts Well: Understanding Object-Sensitivity被提出。

需要注意的是，是 allocation site 所处的类的类型，不是接收对象的类型。例如，在下面这段代码中：

1 class X {
2     void m() {
3         Y y = new Y();
4     }
5 }

$Intype(o_3) = X$ 而非 $Y$

因为这种方式本质上是 Object-Sensitivity 的省略，因此在相同 k-limiting 条件下，type sensitivity 的准确性 不高于 object sensitivity，但实践上来说，准确率并不会下降太多！

静态分析在安全领域的应用¶

Dorothy E. Denning于 1976 年在论文A Lattice Model of Secure Information Flow提出，一个系统需要访问（access）和流（flow）控制来满足所有安全要求。

访问控制（access control）用来确保程序有权限访问特定信息，主要关心信息是如何被访问的。

信息流安全则是一种端到端的思路，通过追踪信息流通过一个程序的过程，确保该程序能够安全地处理信息，主要关心信息是如何被传播的。

Dorothy E. Denning 与 Peter J. Denning 夫妇二人 1977 年的论文Certification of Programs for Secure Information Flow对信息流做了如下解释：如果变量 x 中的信息被传送到变量 y，它们之间就建立了一条信息流 $x→y$。这看起来与我们前面学过的指针分析十分相似。

一种将信息流和安全联系起来的思路是，将不同类型的变量划分到不同的安全等级（security levels），在这些等级之间建立允许的流，从而形成信息流策略。不同实际场景下的安全等级千差万别，可以很复杂也可以很简单。

考虑最简单的情况：只有 H（高）和 L（低）两个安全等级，下面两行代码就分别对应了这两个等级：

h = getPassword(); // h is high security
broadcast(l); // l is low security

另外，我们也可以在格（lattice）上对安全等级进行建模（来自前面提到的第一篇论文）：$L \leq H$

所谓“信息流策略”，用来限制信息流在不同安全等级之间的流动。例如，J. A. Goguen 和 J. Meseguer 于 1982 年在论文Security Policies and Security Models中提出了一个信息流策略——不干涉策略（noninterference policy），它要求高安全等级的变量中的信息不应对低安全等级的变量中的信息有任何影响。因此，你也不应该能通过观察低安全等级的变量来获得任何高安全等级的信息。对应到代码上，形如 $x_L = y_H$ 这样的语句就违背了这一信息流策略。

在格的视角下，上述策略可以表达为，应确保信息在安全等级的格中向上流动。

机密性（Confidentiality）和完整性（Integrity）

众所周知，信息安全三要素包括机密性（confidentiality）、完整性（integrity）和可用性（availability）。本节课讨论的是信息流，因此重点关注前两个要素。

确保机密性，通俗意义上就是阻止敏感信息泄露；
确保完整性，就是避免不受信的信息污染了受信（重要）的信息（这一说法来自 Ken Biba 于 1977 年发表的论文Integrity Considerations for Secure Computer Systems）。

常见的各种注入问题就是损害了完整性。

有意思的是，结合前面讨论的安全等级相关的知识来看，机密性和完整性恰好是对称的：

确保机密性，就是要避免高安全等级的秘密信息流向低安全等级的公开区域，属于 读保护；
确保完整性，就是要避免低安全等级的不可信信息流向高安全等级的可信区域，属于 写保护。

另外，完整性本身也是一个覆盖广泛的概念。它可以包括数据的正确性（correctness）、完全性（completeness）和一致性（consistency）。

显式流（Explicit Flows）和隐蔽信道（Covert Channels）

我们继续来讨论信息流。“信息”本身是一个抽象的概念，它并不等同于数据。信息可能会有两种不同的传播方式：显式流和隐式流（implicit flow）。

显式流很简单，例如，$x_L = y_H$ 这个语句就是通过直接复制/赋值的方式实现信息传递
隐式流则不那么直观，基于此途径的敏感信息泄露也相对而言不那么好防御。现实中已经有许多这样的例子。例如，在下面的代码片段中，根据 public_L 的结果，我们将能够推断 secret_H的正负性：

secret_H = getSecret();
if (secret_H < 0) publik_L = 1;
else publik_L = 0;

敏感信息虽然没有直接传播，但是它影响了控制流，这可能会被低安全等级的观察者观察到。

通过计算系统传递信息的机制被称作信道（channels）。在此基础上，Butler W.Lampson 于 1973 年发表的文章A Note on the Confinement Problem将那些利用本非用于信息传递的机制的信道称为隐蔽信道。一些常见的隐蔽信道包括：

隐式流，通过程序控制结构传递信息。
终止（termination）信道，通过程序的（不）可终止性差异传递信息。
时间（timing）信道，通过计算时间的差异传递信息。
异常（exceptions），通过异常来传递信息。

尽管隐蔽信道比较难识别和防御，它能够传递的信息通常也比显式流少得多。因此，本课程主要关注显式流。一个问题是，如何检测和避免非预期的信息流呢？接下来将要讨论的污点分析是有效的解决方案之一。

污点分析¶

污点分析是最常见的信息流分析技术之一。它将程序数据分为两类：

感兴趣的数据，带有某些标签，也叫做污点数据。
其他数据，或者叫无污点数据。

污点数据的源头称为 sources。实际场景中，污点数据通常来自某些方法的返回值。

污点分析技术将追踪污点数据在程序中的流动过程，观察它们是否流到我们感兴趣的地方（locations of interest），这些地方又称作 sinks。实际场景中，sinks 通常是一些敏感方法（e.g. log()、print()）。

前面我们提到过损害机密性的敏感数据泄露威胁和损害完整性的注入威胁，事实上，污点分析能够用来发现这两类威胁。对于前者来说，source 是敏感数据的来源，sink 是泄露点；对于后者来说，source 是不受信数据的来源，sink 是重要的计算语句（如eval函数）。下面的两段代码分别展示了这两个场景：

// information leak
x = getPassword(); // source
y = x;
log(y); // sink

// injection error
x = readInput(); // source
cmd = "..." + x;
execute(cmd); // sink

污点分析要回答的问题是，某个特定的污点数据能否流到某个 sink 处，或者从另一个角度来看，在一个 sink 处某个指针能够指向哪些污点数据。

Neville Grech 和 Yannis Smaragdakis 于 2017 年发表的论文P/Taint: Unified Points-to and Taint Analysis指出，污点分析可以基于指针分析进行，因为两者非常相似——前者考察的是污点数据如何在程序中流动，后者考察的是抽象对象如何在程序中流动。我们只需要将污点数据当作一种特殊的“人造”对象，将 sources 当作污点数据的 allocation sites，然后应用指针分析来传播污点数据即可。

事实上，上节课学习的上下文敏感的指针分析也可以用于污点分析，从而提高分析精度。不过，谭老师后面并没有给出上下文敏感的分析案例，而是用一个简单的上下文不敏感分析来讲解。

污点分析的域和记法与指针分析基本相同，除了新增的污点数据部分：

Objects: $o_i,o_j \in O$
Tainted data: $t_i,t_j \in T \in O$

其中，$t_i$ 表示污点数据来自 call site $i$。

污点分析的输入如下：

Sources：由 source 方法（被调用后返回污点数据的方法）组成的集合。
Sinks：由携带敏感实参的 sink 方法（污点数据流向这些方法的实参，违背了安全策略）组成的集合。

污点分析的输出是 TaintFlows，它是由“source 和 sink 方法调用构成的元组”组成的集合：$<i,j,k> \in TaintFlows$ 代表污点数据可能会从 call site $i$ （又称为 soucce method）流向 call site $j$ （又被称为 sink method）的第 $k$ 个参数。

污点分析的规则与指针分析基本相同，除了新增的两条处理 sources 和 sinks 的规则：

taint-analysis-role

污点分析新增的规则均应用于 Call 指令上：

若调用的方法属于 Sources，则创建污染节点 $t_l$，并让指针 $r$ 指向它，即 $t_i \in pt(r)$
若调用的方法属于 Sinks，且若存在一个参数，其指向污染节点 $ti \in pt(a_I)$，则说明发现了一条 sources 到 sink 的传播，将其记载入 TaintFlows 中。

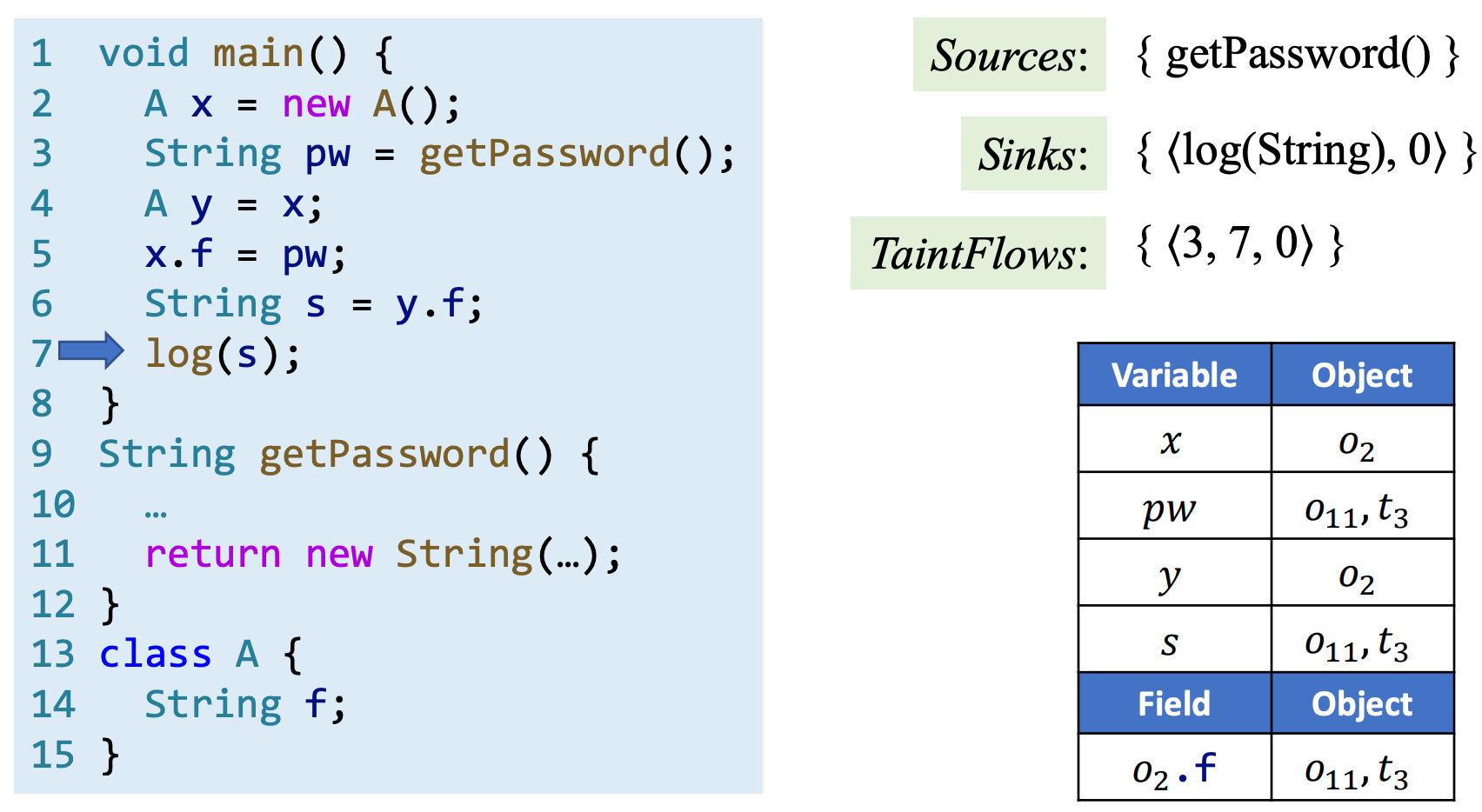
taint-analysis-example

当执行第七行 log(s) 时，由于该方法是 sink 方法，且其参数 s 指向污染节点 $t_3$，因此说明发现了一条 source 到 sink 的传播，将其记录为 TaintFlow $<3,7,0>$ 。

基于 Datalog 的静态分析¶

在之前的实验中，我们都是用 Java 编程实现相关的分析。包括 Java 在内，大多数编程语言都是命令式（imperative）的，我们通过编程来告诉计算机一步步需要做什么。除了命令式语言外，还有一类声明式（declarative）的语言，如 SQL、Prolog和本节将要介绍的Datalog。我们可以简单认为 Datalog 语言是升级版 SQL 语言，同时在语法层面又是 Prolog 语言的子集。

下面两个代码片段实现了相同的功能，但分别采用了命令式语言和声明式语言。

首先是命令式：

Set<Person> selectAdults(Set<Person> persons) {
    Set<Person> result = new HashSet<>();
    for (Person person : persons)
        if (person.getAge() >= 18)
            result.add(person);
    return result;
}

接着是声明式：

SELECT * FROM Persons WHERE Age >= 18;

可以看出，声明式语言的代码更为简洁，忽略了很多实现相关、算法无关的细节。事实上，使用 Datalog 这种声明式语言来实现程序分析算法也要比使用命令式语言简单，最终产物也更简洁、可读。

Datalog，拆开就是 Data+Logic，它有四个特点：无副作用，无控制流，无函数，非图灵完备。

Predicates (Data)¶

在 Datalog 中，predicate（谓词） 是一个声明集合，可以类比为数据表。

一个 fact 则是针对某个特定 tuple 是否属于一个关系的断言——针对给定的值的组合，某 predicate 为真。

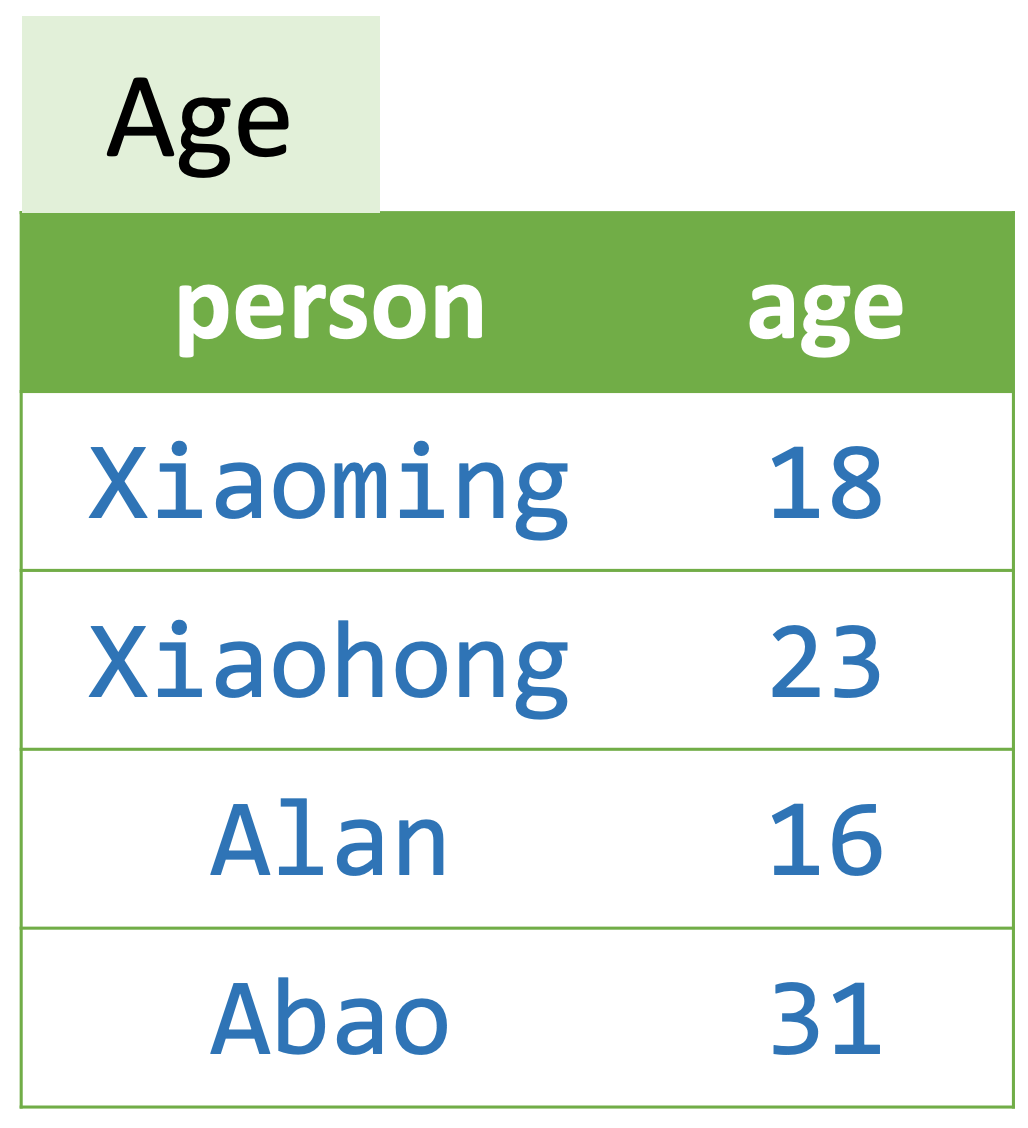
Predicates-Data

如图所示，假设有一个 predicate（table）是 Age，包含 person 和 age 两个 column，那么("Xiaoming", 18)为真（fact），因为这个元组存在于 Age predicate 中；而 ("Alan", 18) 不是真（fact）。

Atoms¶

Atoms 是 Datalog 中的基本元素，用来以下面这种形式表示 predicate：

P(X1, X2, ..., Xn)

其中 P 是 predicate 名，后面跟的 X1 ～ Xn 是 arguments（terms）。Terms 可以是 Variables（变量）或 Constants（常量）。

例如，Age("Xiaoming", 18)就是一个 atom。P(X1, X2, ..., Xn)又称作 relational atoms，当且仅当谓词 P 包含 X1 到 Xn 描述的元组时，它才为真。除了 relational atoms 外，Datalog 还有 arithmetic atoms，如age >= 18。

Datalog Rules (Logic)¶

规则是 Datalog 中表示逻辑推理的形式，用于说明 facts 的推导过程。Datalog 中基本的规则形式如下：

H <- B1, B2, ..., Bn.

H 表示 head（consequent），是一个 atom；B1 ～ Bn 表示 body（antecedent），Bi 也是 atom（可以是否定的），每个 Bi 都是一个 subgoal。

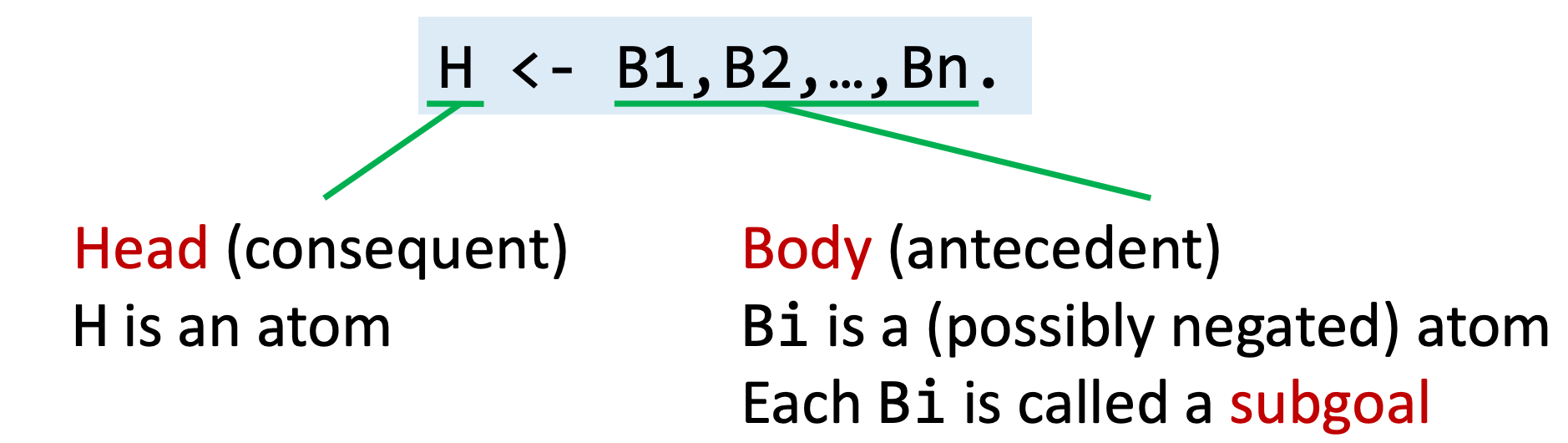
head-body

上述规则的意思是：当 body 为真时，head 为真。

（1）逻辑与

逗号,表示 逻辑与，即，B1 ～ Bn 所有 subgoals 均为真时，body 才为真，继而 head 才为真。例如，我们可以用如下规则推导出成年人：

Adult(person) <- Age(person, age), age >= 18

上述规则的解析过程如下：

考虑所有 subgoals 中的变量的值的所有可能组合。
如果某个组合能够让所有 subgoals 为真，则 head atom 也为真。
head 谓词包含所有 true atoms。

（2）逻辑或

在 Datalog 中有两种方式表示 逻辑或：

一种方式是用分号;连接
另一种方式是写多个 head 相同的规则。

需要注意的是，Datalog 中也有运算符优先级，“逻辑或”低于“逻辑与”，因此括号有时必不可少。

（3）逻辑否

感叹号!则表示对某 atom 的否定，如!B(...)。

datalog-example

上图是一个解析规则的例子。

那么，初始数据，或者说那些 facts，来自哪呢？

EDB 和 IDB 谓词¶

Datalog 中的谓词分为两部分：EDB（extensional database）和 IDB（intensional database）。前者是预先定义的，作为程序输入，且不可变；后者是由规则创建的，关系由规则推理而来，可以看做程序的输出。

对于一条规则H <- B1, B2, ..., Bn.来说，H 只能是 IDB，Bi 则可以是 EDB 或 IDB。

递归¶

Datalog 支持递归的规则，允许 IDB 谓词的自推导。例如，我们在计算图上的可达性信息（传递闭包）时，就需要递归规则：

Reach(from, to) <- Edge(from, to).
Reach(from, to) <- Reach(from, node), Edge(node, to).

正是递归赋予了 Datalog 超出 SQL 的强大能力。也因此，我们能将其用于复杂程序分析中。

另外注意，下面这样的规则是不可行的：

A(x) <- B(x), !A(x)

它是自相矛盾而无意义的。例如，在B(1)为真时，如果A(1)为真，则得出A(1)为假，反过来类似，都是矛盾的。因此，在 Datalog 中，对同一 atom 的递归和否定必须分开，否则该规则可能无法收敛。

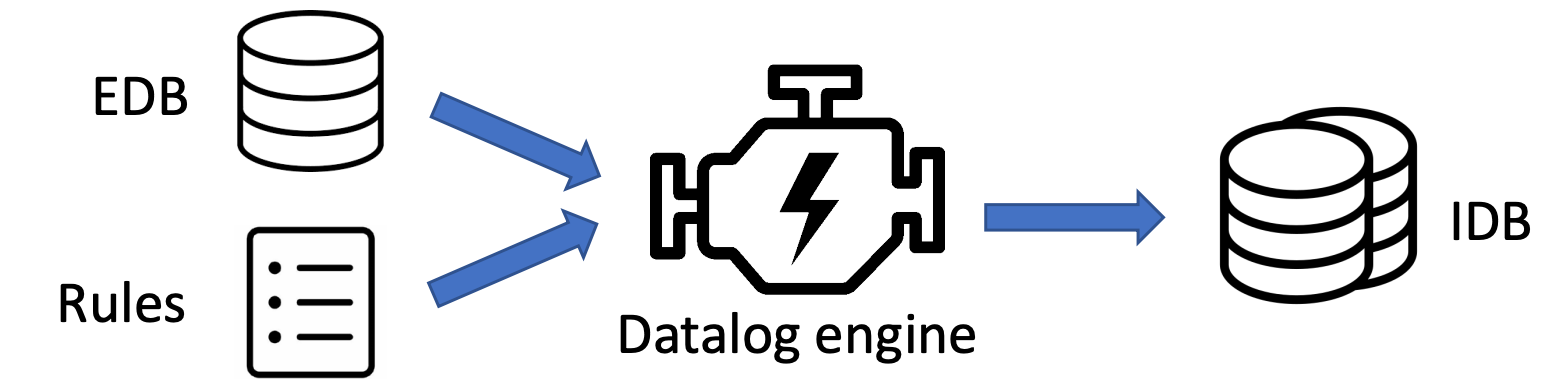
Datalog 程序的执行过程¶

Datalog 引擎的输入是 EDB 和 rules，输出是 IDB。引擎将根据输入来推理 facts，直到没有新 facts 产生。常见的引擎有 LogicBlox、Soufflé、XSB、Datomic 和 Flora-2 等。

我们在之前的学习中提到过单调性。事实上，Datalog 是单调的，也就是说，已经产生的 facts 不会被删除。

我们说 Datalog 程序是可终止的，因为：Datalog 是单调的，且在规则安全的前提下，IDB 谓词的可能值是有限的。

EDB-IDB

不安全的语句¶

需要注意的是，下述规则是不安全的（因此也不被 Datalog 允许）：

A(x) <- B(y), x > y.
A(x) <- B(y), !C(x, y).
A(x) <- B(x), !A(x).

为什么它们是不安全的？因为这两个规则都没有对 x 进行有效限制，意味着可以满足规则的 x 是无限的，这将导致 A 是一个无穷尽的关系。第二个规则可能具有一些迷惑性，但是它确实也是不安全的——也许C(x, y)对 x 进行了限制，但是对它取否定则导致 x 无限制。只有当规则内的每个变量至少出现在一个非否定的关系 atom 中时，这个规则才是安全的。

第三个规则则会造成自反递归，且无意义。

基于 Datalog 的指针分析¶

下面，我们来研究一下如何基于 Datalog 实现（上下文不敏感的）指针分析。首先明确一下输入输出：

规则：指针分析规则，包括 New、Assign、Store、Load（先不考虑 Call 规则）。
EDB：从程序中提取的指针相关的信息，包括：
New(x:V, o:O)
Assign(x:V, y:V)
Store(x:V, f:F, y:V)
Load(y:V, x:V, f:F)
IDB：指针分析结果，包括：
VarPointsTo(v : V, o : O)
FieldPointsTo(oi : O, f : F, oj : O)

我们结合一个案例来分析：

1 b = new C();
2 a = b;
3 c = new C();
4 c.f = a;
5 d = c;
6 c.f = d;
7 e = d.f;

EDB 输入如下：

EDB-output

下面是之前我们总结的指针分析规则：

pta-role-simple

这些规则对应的 Datalog 规则如下：

VarPointsTo(x, o) <- New(x, o).
VarPointsTo(x, o) <- Assign(x, y), VarPointsTo(y, o).
FieldPointsTo(oi, f, oj) <- Store(x, f, y), VarPointsTo(x, oi), VarPointsTo(y, oj).
VarPointsTo(x, o) <- Load (y, x, f), VarPointsTo(x, oi), FieldPointsTo(oi, f, oj).

Datalog 在实现上的确十分简洁。这里就不展示推理过程了，感兴趣的同学可以自行学习一下课件。

最后来看一下如何处理 Call 规则：

pta-role-call-simple

Call 规则比较复杂，其对应的新增 EDB 如下：

VCall(l:S, x:V, k:M)
Dispatch(o:O, k:M, m:M)
ThisVar(m:M, this:V)
Argument(l:S, i:N, ai:V)
Parameter(m:M, i:N, pi:V)
MethodReturn(m:M, ret:V)
CallReturn(l:S, r:V)

新增的 IDB 如下：

Reachable(m:M)
CallGraph(l:S, m:M)

我们需要三条 Datalog 语句来表示 Call 规则：

VarPointsTo(this, o), Reachable(m), CallGraph(l, m) <- VCall(l, x, k), VarPointsTo(x, o), Dispatch(o, k, m), ThisVar(m, this).
VarPointsTo(pi, o) <- CallGraph(l, m), Argument(l, i , ai), Parameter(m, i, pi), VarPointsTo(ai, o).
VarPointsTo(r, o) <- CallGraph(l, m), MethodReturn(m, ret), VarPointsTo(ret, o), CallReturn(l, r).

最终，针对之前的代码段，我们得出如下 Datalog 分析规则：

Reachable(m) <- EntryMethod(m).
VarPointsTo(x, o) <- Reachable(m), New(x, o, m).
VarPointsTo(x, o) <- Assign(x, y), VarPointsTo(y, o).
FieldPointsTo(oi, f, oj) <- Store(x, f, y), VarPointsTo(x, oi), VarPointsTo(y, oj).
VarPointsTo(x, o) <- Load (y, x, f), VarPointsTo(x, oi), FieldPointsTo(oi, f, oj).
VarPointsTo(this, o), Reachable(m), CallGraph(l, m) <- VCall(l, x, k), VarPointsTo(x, o), Dispatch(o, k, m), ThisVar(m, this).
VarPointsTo(pi, o) <- CallGraph(l, m), Argument(l, i , ai), Parameter(m, i, pi), VarPointsTo(ai, o).
VarPointsTo(r, o) <- CallGraph(l, m), MethodReturn(m, ret), VarPointsTo(ret, o), CallReturn(l, r).

注意，我们在开头增加了规则，用于把 entry 加入到 Reachable 中，实现初始化。

基于 Datalog 的污点分析¶

在指针分析的基础上，我们来研究一下如何基于 Datalog 实现污点分析。

结合之前学习的污点分析流程，我们额外增加的 EDB 谓词如下：

Source(m:M)
Sink(m:M, i:N)
Taint(l:S, t:T)

新增的 IDB 谓词如下：

TaintFlow(sr:S, sn:S, i:N)

其中i:N表示 sink call site 的第 i 个参数。

taint-analysis-role

对此，我们新增两条 Datalog 规则：

VarPointsTo(r, t) <- CallGraph(l, m), Source(m), CallReturn(l, r), Taint(l, t).
TaintFlow(j, l, i) <- CallGraph(l, m), Sink(m, i), Argument(l, i, ai), VarPointsTo(ai, t), Taint(j, t).

总结与思考¶

可以发现，Datalog 的优点很明显：简洁、可读、易于实现。另外，Datalog 引擎的性能将直接影响到程序分析效果。它的缺点同样明显：无法充分表达某些逻辑（例如，非全程单调的分析），另外其性能是无法充分控制的，受引擎限制。